题目内容
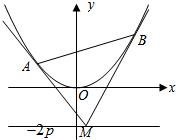 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.(Ⅰ)求证:A,M,B三点的横坐标成等差数列;
(Ⅱ)已知当M点的坐标为(2,-2p)时,|AB|=4
| 10 |
(Ⅲ)是否存在点M,使得点C关于直线AB的对称点D在抛物线x2=2py(p>0)上,其中,点C满足
| OC |
| OA |
| OB |
分析:(Ⅰ)根据题意先设出A,B和M的坐标,对抛物线方程求导,进而表示出AM,BM的斜率,则直线AM和BM的直线方程可得,联立后整理求得2x0=x1+x2.推断出A,M,B三点的横坐标成等差数列.
(Ⅱ)利用(Ⅰ)的结论,x0=2代入抛物线方程整理推断出x1,x2是方程x2-4x-4p2=0的两根,利用韦达定理求得x1+x2的值,表示出直线AB的方程,利用弦长公式求得|AB|,进而求得p,则抛物线的方程可得.
(Ⅲ)设出D点的坐标,进而表示出C的坐标,则CD的中点的坐标可得,代入直线AB的方程,把D点坐标代入抛物线的方程,求得x3,然后讨论x0=0和x0≠0时,两种情况,分析出答案.
(Ⅱ)利用(Ⅰ)的结论,x0=2代入抛物线方程整理推断出x1,x2是方程x2-4x-4p2=0的两根,利用韦达定理求得x1+x2的值,表示出直线AB的方程,利用弦长公式求得|AB|,进而求得p,则抛物线的方程可得.
(Ⅲ)设出D点的坐标,进而表示出C的坐标,则CD的中点的坐标可得,代入直线AB的方程,把D点坐标代入抛物线的方程,求得x3,然后讨论x0=0和x0≠0时,两种情况,分析出答案.
解答:解:(Ⅰ)证明:由题意设A(x1,
),B(x2,
),x1<x2,M(x0,-2p).
由x2=2py得y=
,得y′=
,
所以kMA=
,kMB=
.
因此直线MA的方程为y+2p=
(x-x0),
直线MB的方程为y+2p=
(x-x0).
所以
+2p=
(x1-x0),①
+2p=
(x2-x0).②
由①、②得
=x1+x2-x0,
因此x0=
,即2x0=x1+x2.
所以A,M,B三点的横坐标成等差数列.
(Ⅱ)解:由(Ⅰ)知,当x0=2时,
将其代入①、②并整理得:x12-4x1-4p2=0,x22-4x2-4p2=0,
所以x1,x2是方程x2-4x-4p2=0的两根,
因此x1+x2=4,x1x2=-4p2,
又kAB=
=
=
,
所以kAB=
.
由弦长公式得|AB|=
=
.
又|AB|=4
,
所以p=1或p=2,
因此所求抛物线方程为x2=2y或x2=4y.
(Ⅲ)解:设D(x3,y3),由题意得C(x1+x2,y1+y2),
则CD的中点坐标为Q(
,
),
设直线AB的方程为y-y1=
(x-x1),
由点Q在直线AB上,并注意到点(
,
)也在直线AB上,
代入得y3=
x3.
若D(x3,y3)在抛物线上,则x32=2py3=2x0x3,
因此x3=0或x3=2x0.
即D(0,0)或D(2x0,
).
(1)当x0=0时,则x1+x2=2x0=0,此时,点M(0,-2p)适合题意.
(2)当x0≠0,对于D(0,0),此时C(2x0,
),kCD=
=
,
又kAB=
,AB⊥CD,
所以kAB•kCD=
•
=
=-1,
即x12+x22=-4p2,矛盾.
对于D(2x0,
),因为C(2x0,
),此时直线CD平行于y轴,
又kAB=
≠0,
所以直线AB与直线CD不垂直,与题设矛盾,
所以x0≠0时,不存在符合题意的M点.
综上所述,仅存在一点M(0,-2p)适合题意.
| ||
| 2p |
| ||
| 2p |
由x2=2py得y=
| x2 |
| 2p |
| x |
| p |
所以kMA=
| x1 |
| p |
| x2 |
| p |
因此直线MA的方程为y+2p=
| x1 |
| p |
直线MB的方程为y+2p=
| x2 |
| p |
所以
| ||
| 2p |
| x1 |
| p |
| ||
| 2p |
| x2 |
| p |
由①、②得
| x1+x2 |
| 2 |
因此x0=
| x1+x2 |
| 2 |
所以A,M,B三点的横坐标成等差数列.
(Ⅱ)解:由(Ⅰ)知,当x0=2时,
将其代入①、②并整理得:x12-4x1-4p2=0,x22-4x2-4p2=0,
所以x1,x2是方程x2-4x-4p2=0的两根,
因此x1+x2=4,x1x2=-4p2,
又kAB=
| ||||||||
| x2-x1 |
| x1+x2 |
| 2p |
| x0 |
| p |
所以kAB=
| 2 |
| p |
由弦长公式得|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
1+
|
| 16+16p2 |
又|AB|=4
| 10 |
所以p=1或p=2,
因此所求抛物线方程为x2=2y或x2=4y.
(Ⅲ)解:设D(x3,y3),由题意得C(x1+x2,y1+y2),
则CD的中点坐标为Q(
| x1+x2+x3 |
| 2 |
| y1+y2+y3 |
| 2 |
设直线AB的方程为y-y1=
| x0 |
| p |
由点Q在直线AB上,并注意到点(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
代入得y3=
| x0 |
| p |
若D(x3,y3)在抛物线上,则x32=2py3=2x0x3,
因此x3=0或x3=2x0.
即D(0,0)或D(2x0,
2
| ||
| p |
(1)当x0=0时,则x1+x2=2x0=0,此时,点M(0,-2p)适合题意.
(2)当x0≠0,对于D(0,0),此时C(2x0,
| ||||
| 2p |
| ||||||
| 2x0 |
| ||||
| 4px0 |
又kAB=
| x0 |
| p |
所以kAB•kCD=
| x0 |
| p |
| ||||
| 4px0 |
| ||||
| 4p2 |
即x12+x22=-4p2,矛盾.
对于D(2x0,
2
| ||
| p |
| ||||
| 2p |
又kAB=
| x0 |
| p |
所以直线AB与直线CD不垂直,与题设矛盾,
所以x0≠0时,不存在符合题意的M点.
综上所述,仅存在一点M(0,-2p)适合题意.
点评:本题主要考查了直线与圆锥曲线的关系的综合问题.考查了学生分析推理和分类讨论思想的运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.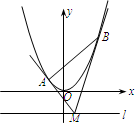 如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B. ,
,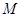 为直线
为直线 上任意一点,过
上任意一点,过 .
.
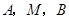 三点的横坐标成等差数列;
三点的横坐标成等差数列;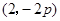 时,
时,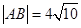 .求此时抛物线的方程。
.求此时抛物线的方程。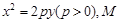 直线
直线 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。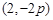 时,
时,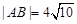 ,求此时抛物线的方程;
,求此时抛物线的方程; 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.