题目内容
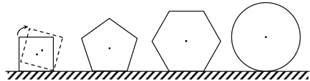
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个，在水平桌面上无滑动滚动一周，它们的中心的运动轨迹长分别为
，
，
，
，则（ ）
A.
B.
C.
D.
【答案】B
【解析】
由题意可知，它们的中心滚动一周的运动轨迹都是圆心角为2π的弧长，设半径分别为r1，r2，r3，r4，则半径为中心与顶点的距离，由正方形、正五边形、正六边形得几何特征可知
，r1＜r2＜1，r3＝r4＝1，再利用弧长公式即可得到l1＜l2＜l3＝l4．
解：由题意可知，它们的中心滚动一周的运动轨迹都是圆心角为2π的弧长，
设半径分别为r1，r2，r3，r4，由题意可知，半径为中心与顶点的距离，
又因为正方形、正五边形、正六边形的边长均为1，圆的半径为1，
对于正方形，如图所示：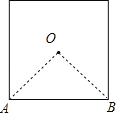
，∵∠AOB＝90°，∴；
对于正五边形，如图所示：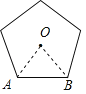
，∵∠AOB＝72°＜90°，∠OAB＝∠OBA＝54°＜72°，∴r1＜r2＜1；
对于正六边形，如图所示：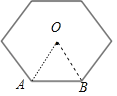
，∠AOB＝60°，∴△AOB为等边三角形，∴r3＝OA＝1；
而 r4＝1，
又因为l1＝2πr1，l2＝2πr2，l3＝2πr3，l4＝2πr4，
所以l1＜l2＜l3＝l4，
故选：B．
名校练考卷期末冲刺卷系列答案
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度y（单位：cm）的情况如下表：
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2019年12月份AQI指数M的频数分布表如下：
M |
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
（1）设
，若x与y之间具有线性关系，试根据上述数据求出y关于x的线性回归方程；
（2）王先生在该市开了一家洗车店，洗车店每天的平均收入与AQI指数的相关关系如下表：
M |
|
|
|
|
|
日均收入（元） | -2000 | -1000 | 2000 | 6000 | 8000 |
估计王先生的洗车店2019年12月份每天的平均收入．
附参考公式：
，其中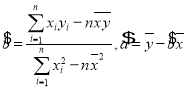
【题目】某校高三（1）班在一次语文测试结束后，发现同学们在背诵内容方面失分较为严重.为了提升背诵效果，班主任倡议大家在早、晚读时间站起来大声诵读，为了解同学们对站起来大声诵读的态度，对全班50名同学进行调查，将调查结果进行整理后制成下表：
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
（1）欲使测试优秀率为30%，则优秀分数线应定为多少分？
（2）依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系，列出2×2列联表，并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据：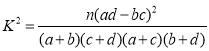
，
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
