题目内容
【题目】已知函数![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设两个极值点分别为![]() ,
,![]() ,
,![]() 证明:
证明:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求出![]() ,令
,令![]() ,则
,则![]() ,分
,分![]() 和
和![]() 两种情况讨论
两种情况讨论
(2)由(1)可知,![]() ,所以
,所以 ,要证:
,要证:![]() ,即证
,即证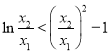 ,然后构造函数
,然后构造函数![]() 即可.
即可.
(1)由题意可知,![]() 的定义域为
的定义域为![]() 且
且![]()
令![]()
则函数![]() 在定义域内有两个不同的极值点等价于
在定义域内有两个不同的极值点等价于
![]() 在区间
在区间![]() 内至少有两个不同的零点
内至少有两个不同的零点
由![]() 可知,
可知,
当![]() 时,
时,![]() 恒成立,即函数
恒成立,即函数![]() 在
在![]() 上单调,不符合题意,舍去.
上单调,不符合题意,舍去.
当![]() 时,由
时,由![]() 得,
得,![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
由![]() 得,
得,![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
故要满足题意,必有![]() 解得:
解得:![]()
(2)证明:由(1)可知,![]() ,所以
,所以
故要证:![]()
即证:![]()
即证: 不妨设
不妨设![]() ,即证
,即证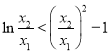
构造函数:![]() ,其中
,其中![]()
由![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 内单调递减,
内单调递减,
所以![]() ,原式得证.
,原式得证.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 20 | 10 | 10 | 20 | 15 | 5 |
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() .某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
.某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
【题目】某公司![]() 人数众多
人数众多![]() 为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,按照男员工和女员工
为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,按照男员工和女员工![]() 的比例分层抽样,得到
的比例分层抽样,得到![]() 名员工的月使用流量
名员工的月使用流量![]() (单位:
(单位:![]() )的数据,其频率分布直方图如图所示.
)的数据,其频率分布直方图如图所示.
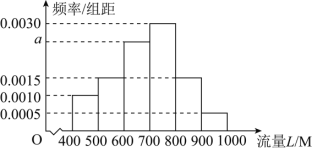
(1)求![]() 的值,并估计这
的值,并估计这![]() 名员工月使用流量的平均值
名员工月使用流量的平均值![]() (同一组中的数据用中点值代表
(同一组中的数据用中点值代表![]() ;
;
(2)若将月使用流量在![]() 以上(含
以上(含![]() )的员工称为“手机营销达人”,填写下面的
)的员工称为“手机营销达人”,填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“成为手机营销达人与员工的性别有关”;
的把握认为“成为手机营销达人与员工的性别有关”;
男员工 | 女员工 | 合计 | |
手机营销达人 | 5 | ||
非手机营销达人 | |||
合计 | 200/span> |
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(3)若这![]() 名员工中有
名员工中有![]() 名男员工每月使用流量在
名男员工每月使用流量在![]() ,从每月使用流量在
,从每月使用流量在![]() 的员工中随机抽取名
的员工中随机抽取名![]() 进行问卷调查,记女员工的人数为
进行问卷调查,记女员工的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】阿尔法狗(AlphaGo)是第一个击败人类职业围棋选手、第一个战胜围棋世界冠军的人工智能程序,由谷歌(Google)公司的团队开发.其主要工作原理是“深度学习”.2017 年5 月,在中国乌镇围棋峰会上,它与排名世界第一的世界围棋冠军柯洁对战,以3 比0 的总比分获胜.围棋界公认阿尔法围棋的棋力已经超过人类职业围棋顶尖水平.
为了激发广大中学生对人工智能的兴趣,某市教育局组织了一次全市中学生“人工智能”软件设计竞赛,从参加比赛的学生中随机抽取了30 名学生,并把他们的比赛成绩按五个等级进行了统计,得到如下数据表:
成绩等级 |
|
|
|
|
|
成绩(分) | 5 | 4 | 3 | 2 | 1 |
人数(名) | 4 | 6 | 10 | 7 | 3 |
(1)根据上面的统计数据,试估计从本市参加比赛的学生中任意抽取一人,其成绩等级为“![]() 或
或![]() ”的
”的
概率;
(2)根据(I)的结论,若从该地区参加比赛的学生(参赛人数很多)中任选3 人,记![]() 表示抽到成绩等级为“
表示抽到成绩等级为“![]() 或
或![]() ”的学生人数,求
”的学生人数,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(3)从这30 名学生中,随机选取2 人,求“这两个人的成绩之差大于1分”的概率.