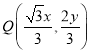题目内容
【题目】狄利克雷函数为F(x)
.有下列四个命题：①此函数为偶函数，且有无数条对称轴；②此函数的值域是
；③此函数为周期函数，但没有最小正周期；④存在三点
，使得△ABC是等腰直角三角形，以上命题正确的是（ ）
A.①②B.①③C.③④D.②④
【答案】B
【解析】
①根据奇偶性定义和对称轴对应的表达式进行判断；②根据
的取值得到值域；③根据周期性的定义进行分析；④先假设存在，然后推理证明是否存在.
①的定义域为
关于原点对称，当
为有理数时，
，当为无理数时，
，
所以
恒成立，所以是偶函数，
取非零有理数
，当为有理数时，
，当为无理数时，，
所以恒成立，有无数种可能，所以有无数条对称轴；
②因为的取值只有
，所以的值域为
；
③取有理数
，当为有理数时，
，当为无理数时，
，
所以
恒成立，有无数种可能，所以是周期函数且无最小正周期；
④设存在
满足条件，
根据函数值域可知，
的可能组合为：两个有理数一个无理数、两个无理数一个有理数，
(1)不妨设
为有理数，
为无理数，因为
为等腰直角三角形，所以
只能为的斜边，
所以
，所以为有理数，与假设矛盾，故不成立；
(2)不妨设为无理数，为有理数，因为为等腰直角三角形，所以只能为的斜边，
所以，所以为无理数，与假设矛盾，故不成立，
综上可知：不存在三点使得为等腰直角三角形.
故选：B.
练习册系列答案
相关题目
