Question

【题目】如图，在四棱锥中，平面，底面是直角梯形，其中，，，，为棱上的点，且．

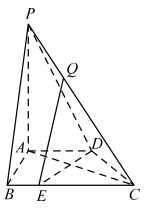
（1）求证：平面；

（2）求二面角的余弦值；

（3）设为棱上的点（不与，重合），且直线与平面所成角的正弦值为，求的值．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）建立适当的空间直角坐标系，确定各点坐标，得到，，根据线面垂直的判定定理，即可证明.

（2）由（1）可知，平面的法向量，确定平面的法向量，根据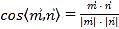，求解即可.

（3）设，确定，，根据直线与平面所成角的正弦值为，求解，即可.

（1）因为平面，平面，平面

所以，

因为

则以A为坐标原点，建立如图所示的空间直角坐标系.

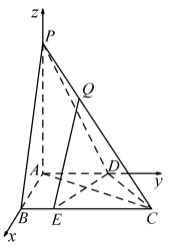
由已知可得，，，，，.

所以，，.

因为，.

所以，

又，平面，平面.

所以平面．

（2）设平面的法向量，由（1）可知，

设平面的法向量

因为，.

所以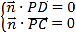，即

不妨设，得．

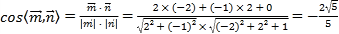
所以二面角的余弦值为．

（3）设，即.

所以，即.

因为直线与平面所成角的正弦值为

所以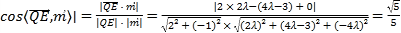

即解得

即．