题目内容
【题目】
已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆的一个顶点,△
是椭圆的一个顶点,△![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上一动点,求线段
上一动点,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 分别作直线
分别作直线![]() ,
,![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为![]() ,
,![]() ,
,
且![]() ,探究:直线
,探究:直线![]() 是否过定点,并说明理由.
是否过定点,并说明理由.
【答案】(1)![]() (2)
(2)![]() (3)直线
(3)直线![]() 过定点(
过定点(![]() ).
).
【解析】
试题(1)求椭圆方程一般利用待定系数法求解,由题意得△![]() 中
中![]() ,因此
,因此![]() ,从而
,从而![]() (2)求轨迹问题,一般根据题意选择对应方法,本题涉及相关点,采取转移法,即设
(2)求轨迹问题,一般根据题意选择对应方法,本题涉及相关点,采取转移法,即设![]() 的中点坐标为
的中点坐标为![]() ,点
,点![]() ,则
,则![]() ,再代入
,再代入![]() ,可得轨迹方程
,可得轨迹方程![]() (3)研究直线过定点问题,一般先利用坐标表示直线方程,再利用方程恒成立问题求相应定点,解题关键为将直线方程表示为点斜式,即将y轴截距用斜率表示
(3)研究直线过定点问题,一般先利用坐标表示直线方程,再利用方程恒成立问题求相应定点,解题关键为将直线方程表示为点斜式,即将y轴截距用斜率表示
试题解析:(1)由已知可得![]() ,所求椭圆方程为
,所求椭圆方程为![]() .
.
(2)设点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() , 则
, 则![]()
![]() 由
由![]() ,
,![]() 得
得![]() 代入上式 得
代入上式 得![]()
(3)若直线![]() 的斜率存在,设
的斜率存在,设![]() 方程为
方程为![]() ,依题意
,依题意![]() .
.
设![]() ,
,![]() ,由
,由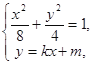 得
得![]() .
.
则![]() . 由已知
. 由已知![]() ,
,
所以![]() ,即
,即![]() .
.
所以![]() ,整理得
,整理得![]() .故直线
.故直线![]() 的方程为
的方程为![]() ,即
,即![]() (
(![]() )
)![]() .所以直线
.所以直线![]() 过定点(
过定点(![]() ).
).
若直线![]() 的斜率不存在,设
的斜率不存在,设![]() 方程为
方程为![]() ,设
,设![]() ,
,![]() ,由已知
,由已知![]() ,得
,得![]() .此时
.此时![]() 方程为
方程为![]() ,显然过点(
,显然过点(![]() ).
).
综上,直线![]() 过定点(
过定点(![]() ).
).

练习册系列答案
相关题目