题目内容
椭圆有两顶点A(﹣1,0)、B(1,0),过其焦点F(0,1)的直线l与椭圆交于C、D两点,并与x轴交于点P.直线AC与直线BD交于点Q.

(Ⅰ)当|CD|= 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A、B两点时,求证: 为定值.
为定值.

(Ⅰ)当|CD|=
 时,求直线l的方程;
时,求直线l的方程;(Ⅱ)当点P异于A、B两点时,求证:
 为定值.
为定值.(Ⅰ)y=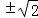 x+1(Ⅱ)见解析
x+1(Ⅱ)见解析
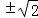 x+1(Ⅱ)见解析
x+1(Ⅱ)见解析试题分析:(Ⅰ)根据椭圆有两顶点A(﹣1,0)、B(1,0),焦点F(0,1),可知椭圆的焦点在y轴上,b=1,c=1,,可以求得椭圆的方程,联立直线和椭圆方程,消去y得到关于x的一元二次方程,利用韦达定理和弦长公式可求出直线l的方程;
(Ⅱ)根据过其焦点F(0,1)的直线l的方程可求出点P的坐标,该直线与椭圆交于C、D两点,和直线AC与直线BD交于点Q,求出直线AC与直线BD的方程,解该方程组即可求得点Q的坐标,代入
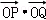 即可证明结论.
即可证明结论.(Ⅰ)∵椭圆的焦点在y轴上,设椭圆的标准方程为
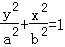 (a>b>0),
(a>b>0),由已知得b=1,c=1,所以a=
 ,
,椭圆的方程为
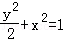 ,
,当直线l与x轴垂直时与题意不符,
设直线l的方程为y=kx+1,C(x1,y1),D(x2,y2),
将直线l的方程代入椭圆的方程化简得(k2+2)x2+2kx﹣1=0,
则x1+x2=﹣
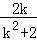 ,x1•x2=﹣
,x1•x2=﹣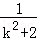 ,
,∴|CD|=
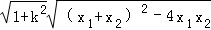 =
=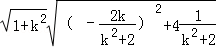
=
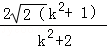 =
=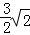 ,
,解得k=
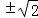 .
.∴直线l的方程为y=
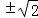 x+1;
x+1;(Ⅱ)证明:当直线l与x轴垂直时与题意不符,
设直线l的方程为y=kx+1,(k≠0,k≠±1),C(x1,y1),D(x2,y2),
∴P点的坐标为(﹣
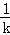 ,0),
,0),由(Ⅰ)知x1+x2=﹣
 ,x1•x2=﹣
,x1•x2=﹣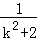 ,
,且直线AC的方程为y=
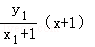 ,且直线BD的方程为y=
,且直线BD的方程为y= ,
,将两直线联立,消去y得
 ,
,∵﹣1<x1,x2<1,∴
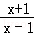 与
与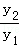 异号,
异号, =
=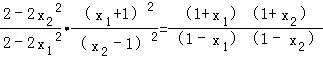
=
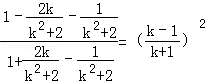 ,
,y1y2=k2x1x2+k(x1+x2)+1=
 =﹣
=﹣ ,
,∴
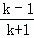 与y1y2异号,
与y1y2异号,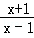 与
与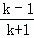 同号,
同号,∴
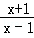 =
=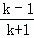 ,解得x=﹣k,
,解得x=﹣k,故Q点坐标为(﹣k,y0),
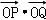 =(﹣
=(﹣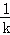 ,0)•(﹣k,y0)=1,
,0)•(﹣k,y0)=1,故
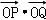 为定值.
为定值.点评:此题是个难题.本题考查了椭圆的标准方程和简单的几何性质、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.体现了分类讨论和数形结合的思想

练习册系列答案
相关题目
 的焦点在
的焦点在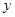 轴上,
轴上, ,
, ,则这样的椭圆个数共有 ( )
,则这样的椭圆个数共有 ( )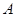 、
、
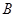 、
、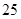
 、
、
 、
、
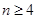 ,
,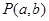 是平面直角坐标系
是平面直角坐标系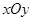 中的点,其中
中的点,其中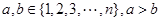
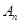 为满足
为满足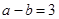 的点
的点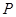 的个数,求
的个数,求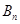 为满足
为满足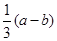 是整数的点
是整数的点 及点
及点 ,在
,在 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 。
。 到线段
到线段 的距离
的距离 所表示图形的面积;
所表示图形的面积;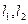 距离相等的点的集合
距离相等的点的集合 ,其中
,其中 ,
,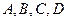 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。 。
。 。
。 。
。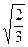 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段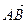 的比为2.
的比为2. :
:
 上的一动点
上的一动点 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长. (
( ,
,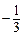 )的动直线
)的动直线 交椭圆
交椭圆 、
、 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论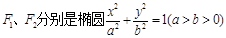 的左、右焦点,
的左、右焦点, 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点 也在椭圆 上,且满足
也在椭圆 上,且满足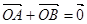 (
(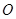 为坐标原点),
为坐标原点),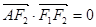 ,若椭圆的离心率等于
,若椭圆的离心率等于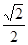 , 则直线
, 则直线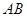 的方程是 ( ▲ ) .
的方程是 ( ▲ ) .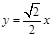
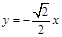
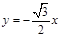
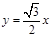
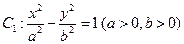 的左、右焦点分别为
的左、右焦点分别为 、
、 ,抛物线
,抛物线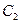 的顶点在原点,它的准线与双曲线
的顶点在原点,它的准线与双曲线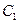 的左准线重合,若双曲线
的左准线重合,若双曲线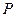 满足
满足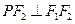 ,则双曲线
,则双曲线 上一点
上一点 到点
到点 的距离是20,则点
的距离是20,则点 的距离是 --------
的距离是 --------