题目内容
(本小题满分13分)
已知椭圆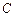 :
:
 上的一动点
上的一动点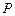 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.
(Ⅰ) 求椭圆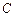 的方程;
的方程;
(Ⅱ) 过点 (
( ,
,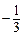 )的动直线
)的动直线 交椭圆
交椭圆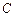 于
于 、
、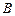 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 如何转动,以
如何转动,以
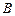 为直径的圆恒过定点
为直径的圆恒过定点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知椭圆
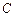 :
:
 上的一动点
上的一动点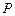 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.(Ⅰ) 求椭圆
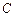 的方程;
的方程;(Ⅱ) 过点
 (
( ,
,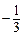 )的动直线
)的动直线 交椭圆
交椭圆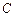 于
于 、
、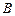 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 如何转动,以
如何转动,以
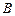 为直径的圆恒过定点
为直径的圆恒过定点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.解: (Ⅰ)设椭圆的焦距为 ,则由题设可知
,则由题设可知 ,解此方程组得
,解此方程组得
 ,
, . 所以椭圆C的方程是
. 所以椭圆C的方程是 . ………5分
. ………5分
(Ⅱ)解法一:假设存在点T(u, v). 若直线l的斜率存在,设其方程为 ,
,
将它代入椭圆方程,并整理,得 .
.
设点A、B的坐标分别为 ,则
,则
因为 及
及
所以

 ……9分
……9分
当且仅当 恒成立时,以AB为直径的圆恒过定点T,
恒成立时,以AB为直径的圆恒过定点T,
所以 解得
解得
此时以AB为直径的圆恒过定点T(0,1). ……11分
当直线l的斜率不存在,l与y轴重合,以AB为直径的圆为 也过点T(0,1).
也过点T(0,1).
综上可知,在坐标平面上存在一个定点T(0,1),满足条件. ……13分
解法二:若直线l与y轴重合,则以AB为直径的圆是
若直线l垂直于y轴,则以AB为直径的圆是 ……7分
……7分
由 解得
解得 .
.
由此可知所求点T如果存在,只能是(0,1). ……8分
事实上点T(0,1)就是所求的点. 证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为 ,
,
过点T(0,1); 当直线l的斜率存在,设直线方程为 ,代入椭圆方程,并整理,得
,代入椭圆方程,并整理,得
设点A、B的坐标为 ,则
,则 ……10分
……10分
因为 ,
,


所以 ,即以AB为直径的圆恒过定点T(0,1).
,即以AB为直径的圆恒过定点T(0,1).
综上可知,在坐标平面上存在一个定点T(0,1)满足条件. ……13分
 ,则由题设可知
,则由题设可知 ,解此方程组得
,解此方程组得 ,
, . 所以椭圆C的方程是
. 所以椭圆C的方程是 . ………5分
. ………5分(Ⅱ)解法一:假设存在点T(u, v). 若直线l的斜率存在,设其方程为
 ,
,将它代入椭圆方程,并整理,得
 .
.设点A、B的坐标分别为
 ,则
,则
因为
 及
及
所以


 ……9分
……9分当且仅当
 恒成立时,以AB为直径的圆恒过定点T,
恒成立时,以AB为直径的圆恒过定点T,所以
 解得
解得
此时以AB为直径的圆恒过定点T(0,1). ……11分
当直线l的斜率不存在,l与y轴重合,以AB为直径的圆为
 也过点T(0,1).
也过点T(0,1).综上可知,在坐标平面上存在一个定点T(0,1),满足条件. ……13分
解法二:若直线l与y轴重合,则以AB为直径的圆是

若直线l垂直于y轴,则以AB为直径的圆是
 ……7分
……7分由
 解得
解得 .
.由此可知所求点T如果存在,只能是(0,1). ……8分
事实上点T(0,1)就是所求的点. 证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为
 ,
,过点T(0,1); 当直线l的斜率存在,设直线方程为
 ,代入椭圆方程,并整理,得
,代入椭圆方程,并整理,得
设点A、B的坐标为
 ,则
,则 ……10分
……10分因为
 ,
,

所以
 ,即以AB为直径的圆恒过定点T(0,1).
,即以AB为直径的圆恒过定点T(0,1). 综上可知,在坐标平面上存在一个定点T(0,1)满足条件. ……13分
略

练习册系列答案
相关题目

 时,求直线l的方程;
时,求直线l的方程; 为定值.
为定值.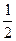 (O为坐标原点).
(O为坐标原点). 轴不垂直时,
轴不垂直时, 点C,使得△ABC为等边三角形,求a
点C,使得△ABC为等边三角形,求a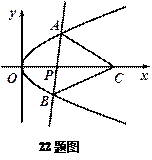
 作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点
作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点 ,若
,若 是等腰三角形,则双曲线的离心率为( )
是等腰三角形,则双曲线的离心率为( )




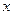 轴为对称轴且经过点
轴为对称轴且经过点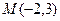 的抛物线的标准方程为___________.
的抛物线的标准方程为___________.
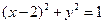 都相切,则双曲线C的离心率是____;
都相切,则双曲线C的离心率是____; 上异于一条直径两个端点的任意一点与这条直径两个端点连线的斜率存在,则这两条直线的斜率乘积为定值-1。写出该定理在有心曲线
上异于一条直径两个端点的任意一点与这条直径两个端点连线的斜率存在,则这两条直线的斜率乘积为定值-1。写出该定理在有心曲线 中的推广 。
中的推广 。