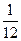题目内容
若函数y=(
)|1-x|+m的图象与x轴有公共点,则m的取值范围是______.
| 1 |
| 2 |
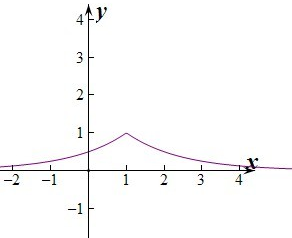
作出函数g(x)=
的图象如图,由图象可知0<g(x)≤1,则m<g(x)+m≤1+m,
即m<f(x)≤1+m,
要使函数y=(
)|1-x|+m的图象与x轴有公共点,则所以与x轴有公共点,
则
,解得-1≤m<0.
故答案为:[-1,0).
|
即m<f(x)≤1+m,
要使函数y=(
| 1 |
| 2 |
则
|
故答案为:[-1,0).


练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 ,若关于
,若关于 的方程
的方程 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则 ( )
( )