题目内容
方程ax+1=-x2+2x+2a，（a＞0，a≠1）的解的个数（ ）
| A．1 | B．2 | C．0 | D．不确定 |
当a＞1时，在同一坐标中画出函数y=ax+1与y=-x2+2x+2a的图象如下图所示
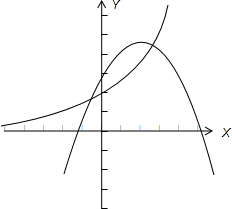
此时两个函数的图象有两个交点，故方程ax+1=-x2+2x+2a有两个解．
当0＜a＜1时，在同一坐标中画出函数y=ax+1与y=-x2+2x+2a的图象如下图所示
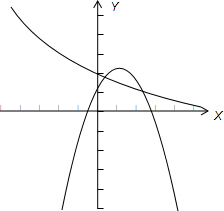
此时两个函数的图象有两个交点，故方程ax+1=-x2+2x+2a有两个解．
综上方程ax+1=-x2+2x+2a有两个解．
故选B．
此时两个函数的图象有两个交点，故方程ax+1=-x2+2x+2a有两个解．
当0＜a＜1时，在同一坐标中画出函数y=ax+1与y=-x2+2x+2a的图象如下图所示
此时两个函数的图象有两个交点，故方程ax+1=-x2+2x+2a有两个解．
综上方程ax+1=-x2+2x+2a有两个解．
故选B．
练习册系列答案
相关题目
，若关于x的方程f2(x)+bf(x)+c=0恰有5个不同的实数解x1,x2,x3,x4,x5,则f(x1+x2+x3+x4+x5)=" " （ ）