Question

【题目】已知等差数列{an}前三项的和为﹣3，前三项的积为8．
（1）求等差数列{an}的通项公式；
（2）若a2 ， a3 ， a1成等比数列，求数列{|an|}的前n项和．

Answer 1

【答案】
（1）解：设等差数列的公差为d，则a2=a1+d，a3=a1+2d

由题意可得，

解得 或

由等差数列的通项公式可得，an=2﹣3（n﹣1）=﹣3n+5或an=﹣4+3（n﹣1）=3n﹣7

（2）解：当an=﹣3n+5时，a2，a3，a1分别为﹣1，﹣4，2不成等比

当an=3n﹣7时，a2，a3，a1分别为﹣1，2，﹣4成等比数列，满足条件

故|an|=|3n﹣7|=

设数列{|an|}的前n项和为Sn

当n=1时，S1=4，当n=2时，S2=5

当n≥3时，Sn=|a1|+|a2|+…+|an|=5+（3×3﹣7）+（3×4﹣7）+…+（3n﹣7）

=5+ = ，当n=2时，满足此式

综上可得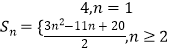

【解析】（1）设等差数列的公差为d，由题意可得， ，解方程可求a1 ， d，进而可求通项（2）由（1）的通项可求满足条件a2 ， a3 ， a1成等比的通项为an=3n﹣7，则|an|=|3n﹣7|= ，根据等差数列的求和公式可求
【考点精析】认真审题，首先需要了解等差数列的通项公式（及其变式）(通项公式：或)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系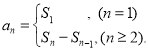)的相关知识才是答题的关键．