题目内容
已知扇形OAB的半径为1，面积为
，设弧AB上有异于A，B的动点C，线段OC与线段AB交于点M，N为OM的中点，则∠AOB=
；若
=x
+y
(x，y∈R)，则x+y=
．
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| ON |
| OA |
| OB |
| 1 |
| 2 |
| 1 |
| 2 |
分析：由扇形OAB的半径为1，面积为
，知
=
，由此能求出∠AOB．由弧AB上有异于A，B的动点C，线段OC与线段AB交于点M，N为OM的中点，取
的中点为C，利用特值法能求出x+y．
| π |
| 3 |
 |
| AB |
| π |
| 3 |
|
| AB |
解答：解：∵扇形OAB的半径为1，面积为
，
∴
=
，
∴∠AOB=
．
∵弧AB上有异于A，B的动点C，线段OC与线段AB交于点M，N为OM的中点，
∴可以取
的中点为C，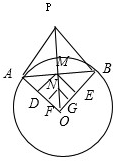
如图，以OA，OB为邻边作平行四边形AOBP，
连接OP，交AB于M，取OA中点D，取OB中点E，取OD中点F，取OE中点G，
则
=
=
+
，
∵
=x
+y
(x，y∈R)，
∴x+y=
．
故答案为：
，
．
| π |
| 3 |
∴
|
| AB |
| π |
| 3 |
∴∠AOB=
| 2π |
| 3 |
∵弧AB上有异于A，B的动点C，线段OC与线段AB交于点M，N为OM的中点，
∴可以取
|
| AB |
如图，以OA，OB为邻边作平行四边形AOBP，
连接OP，交AB于M，取OA中点D，取OB中点E，取OD中点F，取OE中点G，
则
| ON |
| 1 |
| 4 |
| OP |
| 1 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
∵
| ON |
| OA |
| OB |
∴x+y=
| 1 |
| 2 |
故答案为：
| 2π |
| 3 |
| 1 |
| 2 |
点评：本题考查圆心角的求法，考查平面向量的基本运算，解题时要认真审题，注意特殊值的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
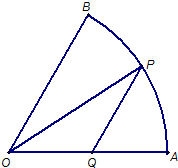已知扇形OAB的半径为3，圆心角∠AOB=60°，过弧AB上的动点P作平行于BO的直线交AO于点Q，设∠AOP=θ．
，求一边在半径上的内接矩形面积的最大值.