题目内容
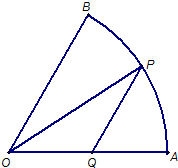 已知扇形OAB的半径为3,圆心角∠AOB=60°,过弧AB上的动点P作平行于BO的直线交AO于点Q,设∠AOP=θ.
已知扇形OAB的半径为3,圆心角∠AOB=60°,过弧AB上的动点P作平行于BO的直线交AO于点Q,设∠AOP=θ.(1)求△POQ的面积S关于θ的函数解析式S=f(θ);
(2)θ为何值时,S=f(θ)有最大值?并求出该最大值.
分析:(1)在三角形POQ中,利用正弦定理列出关系式,表示出OQ,利用三角形面积公式列出函数解析式即可;
(2)将函数解析式积化为差,整理后根据余弦函数的图象与性质即可求出最大值,以及此时θ的度数即可.
(2)将函数解析式积化为差,整理后根据余弦函数的图象与性质即可求出最大值,以及此时θ的度数即可.
解答:解:(1)在△POQ中,由正弦定理得:
=
,即
=
,
∴OQ=2
sin(60°-θ),
则S=
OP•OQ•sin∠POQ=3
sinθsin(60°-θ),θ∈(0,60°);
(2)S=3
sinθsin(60°-θ)=
[cos(2θ-60°)-cos60°]=
[cos(2θ-60°)-
],
则当cos(2θ-60°)=1,即θ=30°时,Smax=
.
| OQ |
| sin∠OPQ |
| OP |
| sin∠OQP |
| OQ |
| sin(60°-θ) |
| 3 |
| sin120° |
∴OQ=2
| 3 |
则S=
| 1 |
| 2 |
| 3 |
(2)S=3
| 3 |
3
| ||
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
则当cos(2θ-60°)=1,即θ=30°时,Smax=
3
| ||
| 4 |
点评:此题考查了正弦定理,三角形的面积公式,余弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目