题目内容
已知扇形OAB的中心角是α=60°，所在圆的半径是R=2，该扇形的面积为
．
| 2π |
| 3 |
| 2π |
| 3 |
分析：求出扇形的弧长，然后求解扇形的面积．
解答：解：因为扇形OAB的中心角是α=60°，即α=
，所在圆的半径是R=2，
所以扇形的弧长为：
，
所以扇形的面积：
×
×2=
．
故答案为：
．
| π |
| 3 |
所以扇形的弧长为：
| 2π |
| 3 |
所以扇形的面积：
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
故答案为：
| 2π |
| 3 |
点评：本题考查扇形的面积公式与扇形的几何计算，基本知识的考查．
练习册系列答案
相关题目
张堰镇为了搞好小区建设美化家园，在新建小区修建一个绿色扇形花坛如图，已知扇形OAB的中心角为4弧度，其面积为2平方米，求扇形的周长和弦AB的长．
＝
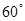，所在圆的半径是R＝2，该扇形的面积为
张堰镇为了搞好小区建设美化家园，在新建小区修建一个绿色扇形花坛如图，已知扇形OAB的中心角为4弧度，其面积为2平方米，求扇形的周长和弦AB的长．