题目内容
已知在 的展开式中,第5项的系数与第3项的系数之比是56:3.
的展开式中,第5项的系数与第3项的系数之比是56:3.
(1)求展开式中的所有有理项;
(2)求展开式中系数绝对值最大的项.
(3)求 的值.
的值.
(1)T1=x5和T7=13400 ,(2)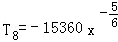 ,(3)
,(3)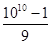 .
.
解析试题分析:(1)求二项展开式中特定项,关键在从通项出发,找寻对应等量关系. 由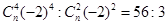 解得n=10,因为通项:
解得n=10,因为通项: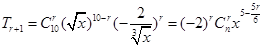 ,当5﹣
,当5﹣ 为整数,r可取0,6,于是有理项为T1=x5和T7=13400,(2)求展开式中系数绝对值最大的项,通过列不等式解决. 设第r+1项系数绝对值最大,则
为整数,r可取0,6,于是有理项为T1=x5和T7=13400,(2)求展开式中系数绝对值最大的项,通过列不等式解决. 设第r+1项系数绝对值最大,则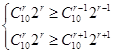 ,解得
,解得 ,于是r只能为7,所以系数绝对值最大的项为
,于是r只能为7,所以系数绝对值最大的项为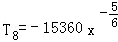 ,(3)本题是二项式定理的逆向应用,关键将式子转化符合二项展开式的特征.
,(3)本题是二项式定理的逆向应用,关键将式子转化符合二项展开式的特征. 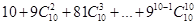
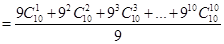
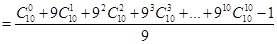
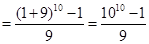
(1)由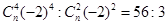 解得n=10 (2分)
解得n=10 (2分)
因为通项: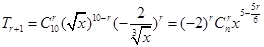 (3分)
(3分)
当5﹣ 为整数,r可取0,6 (4分)
为整数,r可取0,6 (4分)
展开式是常数项,于是有理项为T1=x5和T7=13400 (6分)
(2)设第r+1项系数绝对值最大,则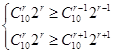 (8分)
(8分)
注:等号不写扣(1分)
解得 ,于是r只能为7 (10分)
,于是r只能为7 (10分)
所以系数绝对值最大的项为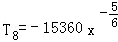 (11分)
(11分)
(3)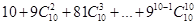
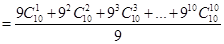
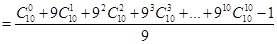 13分
13分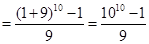 .16分
.16分
考点:二项展开式定理

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 展开式的二项式系数之和为256.
展开式的二项式系数之和为256. ;
; ,求
,求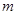 的值;
的值; 展开式中系数最大项只有第6项和第7项,求
展开式中系数最大项只有第6项和第7项,求 -
-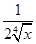 )n的展开式中,前三项系数的绝对值依次成等差数列.
)n的展开式中,前三项系数的绝对值依次成等差数列.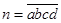 的各位数码
的各位数码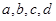 中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义
中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义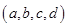 为的数码组,其中
为的数码组,其中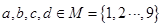 若 数码组为
若 数码组为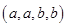 型,
型,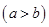 , 试求所有四位三角形数的个数.
, 试求所有四位三角形数的个数. 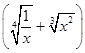 n展开式中的倒数第三项的系数为45,求:
n展开式中的倒数第三项的系数为45,求: