题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]()
![]()
![]() 分别是棱
分别是棱![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上(包括两个端点)运动.
上(包括两个端点)运动.

(1)当![]() 为线段
为线段![]() 的中点时,
的中点时,
①求证:![]() ;②求平面
;②求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值的取值范围.
所成的角的正弦值的取值范围.
【答案】(1)①见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
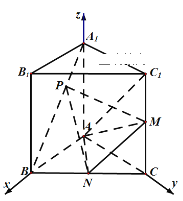
(1)以![]() 为正交基底建立如图所示的空间直角坐标系
为正交基底建立如图所示的空间直角坐标系![]() ,
,
由向量法证明线线垂直和计算二面角。(2)设![]() (
(![]() ),设直线
),设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 由向量坐标法求得
由向量坐标法求得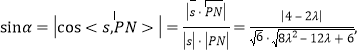
![]() 设
设![]() 设
设![]() 由导数法求得范围。
由导数法求得范围。
以![]() 为正交基底建立如图所示的空间直角坐标系
为正交基底建立如图所示的空间直角坐标系![]() ,
,
则![]()
![]()
![]() ,
,![]() .
.
因为![]() 分别是棱
分别是棱![]() 的中点,所以
的中点,所以![]()
(1)当![]() 为线段
为线段![]() 的中点时,则
的中点时,则![]()
①因为![]()
![]() 所以
所以![]() 即
即![]()
②因为![]() 设平面
设平面![]() 的一个法向量为
的一个法向量为![]()
由![]()
![]() 可得
可得![]() ,取
,取![]() ,则
,则![]() 所以
所以![]()
又因为![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 与平面
与平面![]() 所成的二面角的平面角为
所成的二面角的平面角为![]() ,
,
则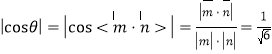
![]() .因为
.因为![]() 为锐角,所以
为锐角,所以![]()
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]()
(2)因为![]() 在线段
在线段![]() 上,所以设
上,所以设![]() (
(![]() ),解得
),解得![]() ,
,
所以![]() .
.
因为![]() 设平面
设平面![]() 的一个法向量为
的一个法向量为![]()
由![]() 可得
可得![]() ,取
,取![]() 则
则![]() 所以
所以![]()
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则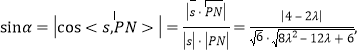
因为![]() 所以
所以![]() 设
设![]() 则
则![]()
所以![]() ,设
,设![]()
则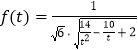 ,设
,设![]() 可求得
可求得![]() 的取值范围为
的取值范围为![]() ,
,
进一步可求得![]() 的取值范围为
的取值范围为![]()
所以直线![]() 与平面
与平面![]() 所成的角的正弦值的取值范围为
所成的角的正弦值的取值范围为![]() .
.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)根据所给的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?附:独立检验临界值表
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |



