题目内容
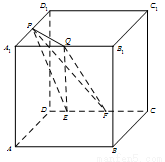
如图,在棱长为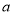 的正方体
的正方体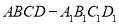 中,
中, 为
为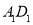 的中点,
的中点,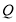 为
为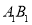 上任意一点,
上任意一点,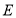 、
、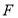 为
为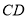 上两点,且
上两点,且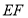 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )
A.点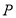 到平面
到平面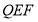 的距离
的距离
B.直线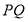 与平面
与平面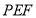 所成的角
所成的角
C.三棱锥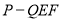 的体积
的体积
D.△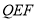 的面积
的面积
练习册系列答案
相关题目
题目内容
如图,在棱长为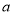 的正方体
的正方体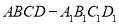 中,
中,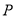 为
为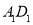 的中点,
的中点,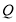 为
为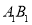 上任意一点,
上任意一点,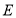 、
、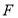 为
为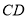 上两点,且
上两点,且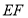 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )

A.点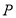 到平面
到平面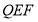 的距离
的距离
B.直线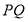 与平面
与平面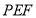 所成的角
所成的角
C.三棱锥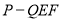 的体积
的体积
D.△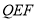 的面积
的面积