题目内容
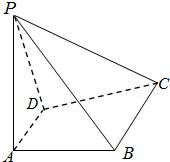 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2AD.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2AD.(1)求证:AB⊥PD;
(2)在线段PB上是否存在一点E,使AE∥平面PCD,若存在,指出点E的位置并加以证明;若不存在,请说明理由.
分析:(1)由PA⊥平面ABCD,推知PA⊥AB.又AB⊥AD,PA∩AD=A,从而有AB⊥平面PAD,证得AB⊥PD.
(2)取线段PB的中点E,PC的中点F,连接AE,EF,DF,则EF是△PBC中位线.可推知四边形EFDA是平行四边形,转化出AE∥DF.再由线面平行的判定定理得证.
(2)取线段PB的中点E,PC的中点F,连接AE,EF,DF,则EF是△PBC中位线.可推知四边形EFDA是平行四边形,转化出AE∥DF.再由线面平行的判定定理得证.
解答: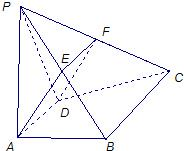 解:
解:
(1)证明∵PA⊥平面ABCD,AB?平面ABCD,
∴PA⊥AB.(2分)
∵AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,(5分)
∵PD?平面PAD,
∴AB⊥PD.(6分)
(2)取线段PB的中点E,PC的中点F,连接AE,EF,DF,
则EF是△PBC中位线.
∴EF∥BC,EF=
BC,
∵AD∥BC,AD=
BC,
∴AD∥EF,AD=EF.
∴四边形EFDA是平行四边形,(8分)
∴AE∥DF.
∵AE?平面PCD,DF?平面PCD,(10分)
∴AE∥平面PCD.(11分)
∴线段PB的中点E是符合题意要求的点.(12分)
∴平面AEF∥平面PCD.(10分)
∵AE?平面AEF,
∴AE∥平面PCD.(11分)
∴线段PB的中点E是符合题意要求的点.(12分)
 解:
解:(1)证明∵PA⊥平面ABCD,AB?平面ABCD,
∴PA⊥AB.(2分)
∵AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,(5分)
∵PD?平面PAD,
∴AB⊥PD.(6分)
(2)取线段PB的中点E,PC的中点F,连接AE,EF,DF,
则EF是△PBC中位线.
∴EF∥BC,EF=
| 1 |
| 2 |
∵AD∥BC,AD=
| 1 |
| 2 |
∴AD∥EF,AD=EF.
∴四边形EFDA是平行四边形,(8分)
∴AE∥DF.
∵AE?平面PCD,DF?平面PCD,(10分)
∴AE∥平面PCD.(11分)
∴线段PB的中点E是符合题意要求的点.(12分)
∴平面AEF∥平面PCD.(10分)
∵AE?平面AEF,
∴AE∥平面PCD.(11分)
∴线段PB的中点E是符合题意要求的点.(12分)
点评:本题主要考查了线面平行与线线平行,线面垂直和线线垂直间的转化,考查了作图能力和转化问题的能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,