题目内容
 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.(1)证明:AE⊥PD;
(2)设AB=2,若H为线段PD上的动点,EH与平面PAD所成的最大角的正切值为
| ||
| 2 |
分析:(1)首先判断四边形ABCD形状,推出△ABC为正三角形,BC边上的中线AE也是高线,联系BC∥AD得到AE⊥AD,再利用AD是PD在平面ABCD内的射影,从而得到AE与PD垂直.
(2)利用AE与PD、PA都垂直,可得到AE⊥平面PAD,从而AE⊥平面AHE,然后求出AE,通过EH与平面PAD所成的最大角的正切值为
.求出AH,最后转到Rt△PAD中求得PA=2.
(2)利用AE与PD、PA都垂直,可得到AE⊥平面PAD,从而AE⊥平面AHE,然后求出AE,通过EH与平面PAD所成的最大角的正切值为
| ||
| 2 |
解答:解:(1)AE⊥PD---------------------------------------(1分)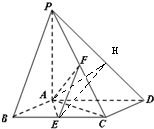
因为四边形ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形.
因为E是BC的中点,
∴AE⊥BC,结合BC∥AD,得AE⊥AD-------------------(2分)
∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE---------(3分)
PA∩AD=A,且PA?平面PAD,AD?平面PAD
∴AE⊥平面PAD,又PD?平面PAD-----------------------------(5分)
∴AE⊥PD-------------------------------------------------(6分)
(2)由(1),EA⊥平面PAD,
∴EA⊥AH,即△AEH为直角三角形,----------(8分)
Rt△EAH中,AE=
,
当AH最短时,即AH⊥PD时,EH与平面PAD所成的角最大,最大角的正切值为
,-----------(10分)
此时,tan∠EHA=
=
,AH=
.
又AD=2,所以∠ADH=45°,所以PA=2.------------------(12分)

因为四边形ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形.
因为E是BC的中点,
∴AE⊥BC,结合BC∥AD,得AE⊥AD-------------------(2分)
∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE---------(3分)
PA∩AD=A,且PA?平面PAD,AD?平面PAD
∴AE⊥平面PAD,又PD?平面PAD-----------------------------(5分)
∴AE⊥PD-------------------------------------------------(6分)
(2)由(1),EA⊥平面PAD,
∴EA⊥AH,即△AEH为直角三角形,----------(8分)
Rt△EAH中,AE=
| 3 |
当AH最短时,即AH⊥PD时,EH与平面PAD所成的角最大,最大角的正切值为
| ||
| 2 |
此时,tan∠EHA=
| AE |
| AH |
| ||
| 2 |
| 2 |
又AD=2,所以∠ADH=45°,所以PA=2.------------------(12分)
点评:本题综合了直线与平面平行的判定、直线与平面垂直的性质和棱柱、棱锥、棱台的体积等几个知识点,属于中档题.在题中出现了探究性问题,请同学们留意在解题过程中“空间问题平面化的思路”,是立体几何常用的数学思想.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,