题目内容
【题目】已知球O为三棱锥S﹣ABC的外接球,![]()
![]() ,则球O的表面积是( )
,则球O的表面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据题意能够求出弦![]() 的中垂面,那么中垂面一定经过球心,设出球心O位置,作
的中垂面,那么中垂面一定经过球心,设出球心O位置,作![]() ⊥平面SAC,可得
⊥平面SAC,可得![]() 为等边三角形SAC的中心,在三角形ABM中求球的半径,需要用到四点共圆的性质解题.
为等边三角形SAC的中心,在三角形ABM中求球的半径,需要用到四点共圆的性质解题.
解:取SC中点M,连接AM、MB,
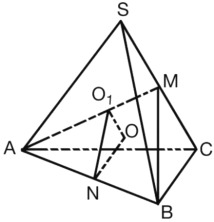
因为△SAC是等边三角形,且SB=BC,
∴AM⊥SC,MB⊥SC,
∴SC⊥平面AMB,
∴球心O在平面AMB上,作![]() ⊥平面SAC,可得
⊥平面SAC,可得![]() 为等边三角形SAC的中心,
为等边三角形SAC的中心,
所以![]() =
=![]() ,
,
取AB中点N,连接ON,∴ON⊥AB,
∴![]() 四点共圆,AO为这四点共圆的直径,也是三棱锥SABC外接球的半径,连接
四点共圆,AO为这四点共圆的直径,也是三棱锥SABC外接球的半径,连接![]() ,
,
在△ABM中:![]() ,
,
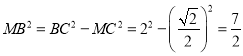 ,
,
![]()
∴∠MAB=90°,
∴在直角三角形![]() 中,
中,
由勾股定理,得![]() =
=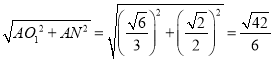 ,
,
∴三棱锥SABC外接球的半径长为AO=![]() =
=![]() ,
,![]() .
.
故选:A.

练习册系列答案
相关题目