Question

【题目】一个三角形数表按如下方式构成（如图：其中项数）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：；为数表中第行的第个数.

…

…

…

……

（1）求第2行和第3行的通项公式和；

（2）证明：数表中除最后2行外每一行的数都依次成等差数列，并求关于的表达式；

（3）若，，试求一个等比数列，使得，且对于任意的，均存在实数，当时，都有.

Answer 1

【答案】（1）。.

（2）见证明；（3）.

【解析】

（1）根据等差数列和等比数列的定义即可求出相应的通项公式，（2）根据条件建立方程关系即可求出f（i，1）的表达式．（3）根据条件寻找等比数列g（i），即可得到结论．

（1）

.

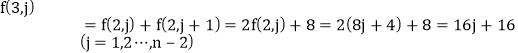（2）由已知，第一行是等差数列，假设第行是以为公差的等差数列，

则由

（常数）知第行的数也依次成等差数列，且其公差为.综上可得，数表中除最后2行以外每一行都成等差数列；

由于，，所以，所以

，由，

得，

于是，

即，又因为，

所以，数列是以2为首项，1为公差的等差数列，

所以，，所以.

（3），

，

令，

.

，

，

，

令，则当时，都有，

∴适合题设的一个等比数列为.