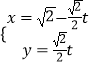题目内容
【题目】已知函数 ![]() (其中ω>0)
(其中ω>0)
(I)求函数f(x)的值域;
(II)若对任意的a∈R,函数y=f(x),x∈(a,a+π]的图象与直线y=﹣1有且仅有两个不同的交点,试确定ω的值(不必证明),并求函数y=f(x),x∈R的单调增区间.
【答案】解:(I)解: ![]() =
= ![]() =
= ![]()
由 ![]() ,得
,得 ![]() 可知函数f(x)的值域为[﹣3,1].
可知函数f(x)的值域为[﹣3,1].
(II)解:由题设条件及三角函数图象和性质可知,y=f(x)的周期为π,
又由ω>0,得 ![]() ,即得ω=2.
,即得ω=2.
于是有 ![]() ,再由
,再由 ![]() ,
,
解得 ![]() .
.
B1所以y=f(x)的单调增区间为 ![]()
【解析】1、根据题意化简函数为一个角的三角函数的形式,根据正弦函数的有界性求出函数f(x)的值域。
2、由已知可得对任意的a∈R,函数y=f(x),x∈(a,a+π]的图象与直线y=﹣1有且仅有两个不同的交点,试确定函数的周期再确定ω的值,然后求函数y=f(x),,x∈R的单调增区间。
【考点精析】通过灵活运用两角和与差的正弦公式,掌握两角和与差的正弦公式:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目