题目内容
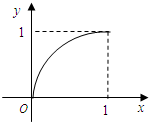已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：①f（x2）-f（x1）＞x2-x1；
②[f（x2）-f（x1）]•（x2-x1）＜0；
③x2f（x1）＞x1f（x2）；
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
其中正确的结论的序号是
分析：根据题意可作出函数y=f（x）的图象，利用直线的斜率的几何意义，利用数形结合的思想研究函数的单调性与最值即可得到答案．
解答：解：由函数y=f（x）的图象可得，
当0＜x1＜x2＜1时，0＜f（x1）＜f（x2）＜1，
[f（x2）-f（x1）]•（x2-x1）＞0，故②错误；
函数y=f（x）在区间[0，1]上的图象如下：
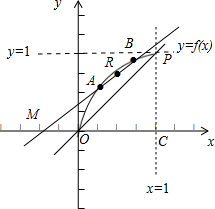
对于①设曲线y=f（x）上两点A（x1，f（x1）），B（x2，f（x2）），直线AB的斜率kAB=
＜kop=1，
∴f（x2）-f（x1）＜x2-x1，故①错误；
对于③，由图可知，koA＞koB，即
＞
，0＜x1＜x2＜1，于是有x2f（x1）＞x1f（x2），故③正确；
对于④，设AB的中点为R，则R（
，
），
的中点为S，则S（
，f(
)），
显然有
＜f(
)，即④正确．
综上所述，正确的结论的序号是③④．
当0＜x1＜x2＜1时，0＜f（x1）＜f（x2）＜1，
[f（x2）-f（x1）]•（x2-x1）＞0，故②错误；
函数y=f（x）在区间[0，1]上的图象如下：
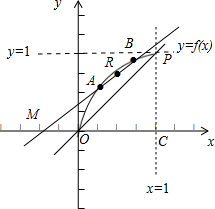
对于①设曲线y=f（x）上两点A（x1，f（x1）），B（x2，f（x2）），直线AB的斜率kAB=
| f(x2)-f(x1) |
| x2-x1 |
∴f（x2）-f（x1）＜x2-x1，故①错误；
对于③，由图可知，koA＞koB，即
| f(x1) |
| x1 |
| f(x2) |
| x2 |
对于④，设AB的中点为R，则R（
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
 |
| AB |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
显然有
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
综上所述，正确的结论的序号是③④．
点评：本题考查函数的图象，着重考查直线的斜率的几何意义，考察函数的单调性，突出考查作图象的能力与数形结合解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知定义在区间[0，2]上的函数y=f（x）的图象如图所示，则y=f（2-x）的图象为（ ）