题目内容
(2011•顺义区二模)已知定义在区间[0,
]上的函数y=f(x)的图象关于直线x=
对称,当x≥
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
| 3π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
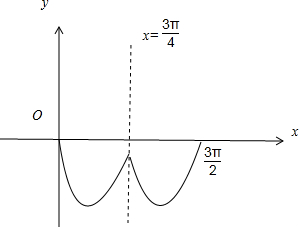
分析:作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案
解答:解:依题意作出在区间[0,
]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0
①当-
<a≤0,f(x)=a有2个解,此时S=
②当a=-
时,f(x)=a有3个解,此时S=0+
+
=
③当-1<a<-
时,f(x)=a有4个交点,此时S=2×
=3π
④a=-1时,f(x)=a有2个交点,此时S=
+
=
故选A
| 3π |
| 2 |
①当-
| ||
| 2 |
| 3π |
| 2 |
②当a=-
| ||
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |
| 9π |
| 4 |
③当-1<a<-
| ||
| 2 |
| 3π |
| 2 |
④a=-1时,f(x)=a有2个交点,此时S=
0+
| ||
| 2 |
| ||||
| 2 |
| 3π |
| 2 |
故选A

点评:本题考查的知识点是函数解析式的求法及函数图象变换法,根的存在性及根的个数的判断,其中根据 y=f(x)的图象关于直线对称.根据对称变换法则,画出出函数的图象是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
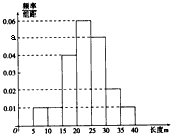 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=