题目内容
填空题
(1)已知
=
,则sin2x的值为
.
(2)已知定义在区间[0,
]上的函数y=f(x)的图象关于直线x=
对称,当x≥
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为
(3)设向量
,
,
满足
+
+
=
,(
-
)⊥
,
⊥
,若|
|=1,则|
|2+|
|2+|
|2的值是
(1)已知
| cos2x | ||
sin(x+
|
| 4 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
(2)已知定义在区间[0,
| 3π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
(-1,-
)
| ||
| 2 |
(-1,-
)
.
| ||
| 2 |
(3)设向量
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| a |
| a |
| b |
| c |
4
4
.分析:(1)利用三角函数的恒等变换化简已知条件可得cos(
+x)=
,由sin2x=-cos(
+2x),利用二倍角的余弦公式求出结果.
(2)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案.
(3)由条件求得 |
|=1,|
|=1,再由得
2=[-(
+
)]2=
2+
2+2
•
=2,即可求得值.
| π |
| 4 |
| 2 |
| 3 |
| π |
| 2 |
(2)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案.
(3)由条件求得 |
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| a |
| b |
解答:解:(1)∵
=
=
=
=2cos(
+x),
∴cos(
+x)=
,∴sin2x=-cos(
+2x)=-[2cos2(
+x)-1]=-(-
)=
,
故答案为
.
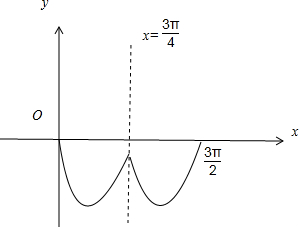
(2)依题意作出函数y=f(x)在区间[0,
]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0.
①当-
<a≤0,f(x)=a有2个解,②当a=-
时,f(x)=a有3个解,
③当-1<a<-
时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,
故方程f(x)=a有四个不同的解,则实数a的取值范围为(-1,-
),
故答案为 (-1,-
).
(3)由题意可得(
-
)•
=(
-
)•(-
-
)=0,∴
2=
2,|
|=|
|.
再由 |
|=1,可得|
|=1.
再由
•
=0,
=-(
+
) 可得
2=[-(
+
)]2=
2+
2+2
•
=2.
∴|
|2+|
|2+|
|2=4,
故答案为4.
| cos2x | ||
sin(x+
|
| 4 |
| 3 |
sin(
| ||
sin(x+
|
2sin(
| ||||
sin(x+
|
| π |
| 4 |
∴cos(
| π |
| 4 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 9 |
| 1 |
| 9 |
故答案为
| 1 |
| 9 |
(2)依题意作出函数y=f(x)在区间[0,
| 3π |
| 2 |
①当-
| ||
| 2 |
| ||
| 2 |
③当-1<a<-
| ||
| 2 |
故方程f(x)=a有四个不同的解,则实数a的取值范围为(-1,-
| ||
| 2 |
故答案为 (-1,-
| ||
| 2 |

(3)由题意可得(
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
再由 |
| a |
| b |
再由
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| a |
| b |
∴|
| a |
| b |
| c |
故答案为4.
点评:本题主要考查三角函数的恒等变换及化简求值,函数的图象及性质,两个向量的数量积的定义,数量积公式的应用,体现了转化、数形结合、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
某校教务处要对高三上学期期中数学试卷进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
|
第一空得分情况 |
|
第二空得分情况 |
||||
|
得分 |
0 |
3 |
|
得分 |
0 |
2 |
|
人数 |
198 |
802 |
|
人数 |
698 |
302 |
|
第一空得分 |
|
第二空得分 |
|||
|
得分 |
0 |
3 |
得分 |
0 |
2 |
|
人数 |
198 |
802 |
人数 |
698 |
302 |
(Ⅰ)求样本试卷中该题的平均分,并据此估计该校高三学生该题的平均分.
(Ⅱ)该校的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题得分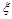 的数学期望.
的数学期望.
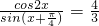 ,则sin2x的值为________.
,则sin2x的值为________.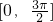 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线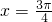 对称,当
对称,当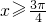 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________.
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________. 满足
满足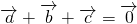 ,
,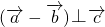 ,
, ,若
,若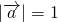 ,则
,则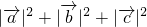 的值是________.
的值是________. ,则sin2x的值为______.
,则sin2x的值为______. 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______