题目内容
【题目】已知函数f(x)= ![]() .
.
(1)求f(x)+f(1﹣x)的值;
(2)若数列{an}满足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1)(n∈N*),求数列{an}的通项公式;
)+f(1)(n∈N*),求数列{an}的通项公式;
(3)若数列{bn}满足bn=2nan , Sn是数列{bn}的前n项和,是否存在正实数k,使不等式knSn>3bn对于一切的n∈N*恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
【答案】
(1)解:∵f(x)= ![]() ,
,
∴ ![]() =
= ![]()
(2)解 ![]() ①
①
∴ ![]() ②
②
由(1),知f(x)+f(1﹣x)=1,
∴①+②,得2an=(n+1),
∴ ![]()
(3)解:因为 ![]() ,
,
∴ ![]() ①
①
2Sn=221+322+423+…+n2n﹣1+(n+1)2n,②
①﹣②得, ![]()
即 ![]() ,
,
要使得不等式knSn>3bn恒成立,
即2kn2>3(n+1)对于一切的n∈N*恒成立,
即 ![]() 对一切的n∈N*恒成立,
对一切的n∈N*恒成立,
令 ![]() ,
,
因为 ![]() 在n∈N*是单调递增的,
在n∈N*是单调递增的,
∴ ![]() 的最小值为2+
的最小值为2+ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴k>3
【解析】(1)由函数f(x)= ![]() ,代入化简,可得f(x)+f(1﹣x)=1,(2)根据(1)中结论,利用倒序相加法,可得
,代入化简,可得f(x)+f(1﹣x)=1,(2)根据(1)中结论,利用倒序相加法,可得 ![]() ;(3)根据(2)中结论,利用错位相减法,可得Sn的表达式,进而再由孤立参数法,可得k的取值范围;
;(3)根据(2)中结论,利用错位相减法,可得Sn的表达式,进而再由孤立参数法,可得k的取值范围;
【考点精析】本题主要考查了函数的值和数列的前n项和的相关知识点,需要掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法;数列{an}的前n项和sn与通项an的关系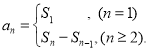 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目