题目内容
为了防止受到核污染的产品影响我国民众的身体健康,要求产品进入市场前必须进行两轮核放射检测,只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为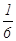 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响。
,两轮检测是否合格相互没有影响。
(1)求该产品不能销售的概率
(2)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利-80元)。已知一箱中有4件产品,记可销售的产品数为X,求X的分布列,并求一箱产品获利的均值。
(1)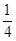 (2)分布列为
(2)分布列为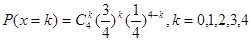 ,获利均值为40
,获利均值为40
解析试题分析:(1)设第一轮检测不合格为事件A,第二轮检测不合格为事件B,A与B相互独立,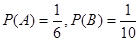 .
.
该产品不能销售的概率为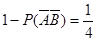 .
.
(2)X的可能取值为0,1,2,3,4. ,分布列为
,分布列为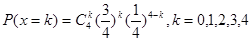 。
。
设一箱产品获利为Y元,则Y=40X-80(4-X)=120X-320。所以E(Y)=120E(X)-320=40.
考点:相互独立事件同时发生的概率及分布列期望
点评:求离散型随机变量分布列首先找到随机变量可以取得值,再根据问题情境求出各值对应的概率,即可写出分布列求出期望

练习册系列答案
相关题目
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
 | 160 | 178 | 166 | 175 | 180 |
 | 75 | 80 | 77 | 70 | 81 |
(2)若
 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望.  ,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力. ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求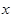 的分布列及期望。
的分布列及期望。 ,求
,求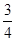 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是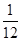 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是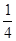 .
. ,求:
,求: 上的概率;
上的概率;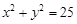 外的概率。
外的概率。 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。 ,求
,求
 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 。
。  ,求
,求