题目内容
已知实数a,b满足:关于x的不等式|x2+ax+b|≤|2x2-4x-16|对一切x∈R均成立.
(1)请验证a=-2,b=-8满足题意.
(2)求出所有满足题意的实数a,b,并说明理由.
(3)若对一切x>2,均有不等式x2+ax+b≥(m+2)x-m-15成立,求实数m的取值范围.
(1)请验证a=-2,b=-8满足题意.
(2)求出所有满足题意的实数a,b,并说明理由.
(3)若对一切x>2,均有不等式x2+ax+b≥(m+2)x-m-15成立,求实数m的取值范围.
(1)见解析 (2)a=-2,b=-8,理由见解析 (3) (-∞,2]
(1)当a=-2,b=-8时,有
|x2+ax+b|=|x2-2x-8|≤2|x2-2x-8|
=|2x2-4x-16|.
(2)在|x2+ax+b|≤|2x2-4x-16|中,
分别取x=4,x=-2,
得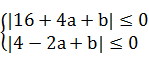 ,所以
,所以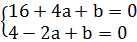 ,
,
所以a=-2,b=-8,
因此满足题意的实数a,b只能是a=-2,b=-8.
(3)由x2+ax+b≥(m+2)x-m-15(x>2),
所以x2-2x-8≥(m+2)x-m-15,
即x2-4x+7≥m(x-1),
所以对一切x>2,均有不等式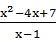 ≥m成立,
≥m成立,
而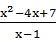 =(x-1)+
=(x-1)+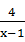 -2
-2
≥2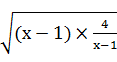 -2=2(当且仅当x=3时等号成立),
-2=2(当且仅当x=3时等号成立),
所以实数m的取值范围是(-∞,2].
|x2+ax+b|=|x2-2x-8|≤2|x2-2x-8|
=|2x2-4x-16|.
(2)在|x2+ax+b|≤|2x2-4x-16|中,
分别取x=4,x=-2,
得
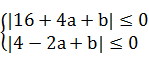 ,所以
,所以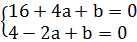 ,
,所以a=-2,b=-8,
因此满足题意的实数a,b只能是a=-2,b=-8.
(3)由x2+ax+b≥(m+2)x-m-15(x>2),
所以x2-2x-8≥(m+2)x-m-15,
即x2-4x+7≥m(x-1),
所以对一切x>2,均有不等式
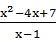 ≥m成立,
≥m成立,而
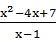 =(x-1)+
=(x-1)+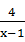 -2
-2≥2
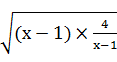 -2=2(当且仅当x=3时等号成立),
-2=2(当且仅当x=3时等号成立),所以实数m的取值范围是(-∞,2].

练习册系列答案
相关题目
 +
+ +2
+2 的最小值是 ( )
的最小值是 ( )
 (x>0)的最小值是 ( )
(x>0)的最小值是 ( )
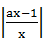 >a的解集为M,且2∉M,则a的取值范围为 ( )
>a的解集为M,且2∉M,则a的取值范围为 ( )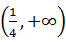
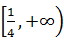
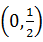
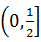
 时,函数y=x2(1-5x)的最大值为 ( )
时,函数y=x2(1-5x)的最大值为 ( )

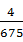
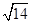 ,求x+y+z的值.
,求x+y+z的值.