题目内容
设x、y、z∈R，且满足x2＋y2＋z2＝1，x＋2y＋3z＝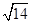
，求x＋y＋z的值．
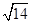，求x＋y＋z的值．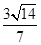
由柯西不等式可知(x＋2y＋3z)2＝14≤(x2＋y2＋z2)·(12＋22＋32)，
因为x2＋y2＋z2＝1，所以当且仅当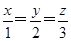
时取等号．
此时y＝2x，z＝3x代入x＋2y＋3z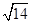＝得x＝
，即y＝
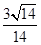，z＝，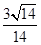
所以x＋y＋z＝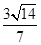
因为x2＋y2＋z2＝1，所以当且仅当
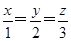时取等号．此时y＝2x，z＝3x代入x＋2y＋3z＝
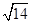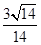得x＝，即y＝，z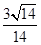＝，所以x＋y＋z＝
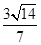
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
≥
＋
.
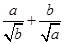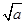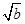∈A，
A.
对
恒成立,则实数
的取值范围是___________.
，则下列不等式中一定成立的是
>b-
同时成立,则ab应满足的条件是 . 
