题目内容
20.在等差数列{an}中,a1=-2015,其前n项和为Sn,若$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2,则S2015的值等于:-2015.分析 由已知推导出{$\frac{{S}_{n}}{n}$}是以-2015为首项,以1为公差的等差数列.由此能求出S2015.
解答 解:设等差数列前n项和为Sn=An2+Bn,
则 $\frac{{S}_{n}}{n}$=An+B,∴{$\frac{{S}_{n}}{n}$}成等差数列.
∵$\frac{{S}_{1}}{1}=\frac{{a}_{1}}{1}$=-2015,∴{$\frac{{S}_{n}}{n}$}是以-2015为首项,以1为公差的等差数列.
∴$\frac{{S}_{2015}}{2015}=-2015+2014×1$=-1,
∴S2015=-2015.
故答案为:-2015.
点评 本题考查数列的前2015项和的求法,是基础题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
10.函数f(x)=ax2+bx-2是定义在[1+a,2]上的偶函数,则f(x)在区间[-1,2]上的值域是( )
| A. | [-10,2] | B. | [-14,-2] | C. | (-∞,-2] | D. | [-14,-5] |
5.已知数列{an}中,a1=3,a2=6,an+2=an+1-an,则a2015=( )
| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
12.今年是我校成立111周年的一年,那么十进制的111化为二进制是( )
| A. | 1 101 101 | B. | 11 011 011 | C. | 1 101 111 | D. | 1 011 100 |
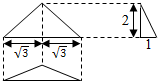 已知一个三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2\sqrt{3}}{3}$.外接球半径为$\sqrt{5}$.
已知一个三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2\sqrt{3}}{3}$.外接球半径为$\sqrt{5}$.
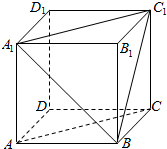 如图,在正方体A1B1C1D1-ABCD中,
如图,在正方体A1B1C1D1-ABCD中,