题目内容
10.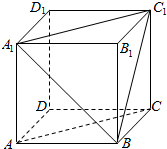 如图,在正方体A1B1C1D1-ABCD中,
如图,在正方体A1B1C1D1-ABCD中,(1)在正方体的12条棱中,与棱AA1是异面直线的有几条(只要写出结果)
(2)证明:AC∥平面A1BC1;
(3)证明:AC⊥平面BDD1B1.
分析 (1)画出正方体ABCD-A1B1C1D1,根据异面直线的概念即可找出与棱AA1异面的棱.
(2)连接AC,A1C1,则A1C1∥AC,利用线面平行的判定定理即可证明;
(3)由DD1⊥面AC,知BD⊥AC,由DD1⊥BD,能够证明AC⊥平面BDD1B1.
解答 解:(1)与棱AA1异面的棱为:CD,C1D1,BC,B1C1,共4条.
(2)证明:连接AC,A1C1,则A1C1∥AC,
∵AC?平面A1BC1,A1C1?平面A1BC1,
∴AC∥平面A1BC1;
(3)证明:∵DD1⊥面AC,AC?平面AC,∴DD1⊥AC,
∵AC⊥BD,DD1∩BD=D,BD?平面BDD1B1,DD1?平面BDD1B1
∴AC⊥平面BDD1B1.
点评 考查异面直线的概念,直线与平面垂直的证明,直线与平面平行的判定,解题时要认真审题,仔细解答,注意合理地进行等价转化,属于中档题.

练习册系列答案
相关题目
18.设a>0,b>1,若a+b=2,则$\frac{2}{a}+\frac{1}{b-1}$的最小值为( )
| A. | $3+2\sqrt{2}$ | B. | 6 | C. | $4\sqrt{2}$ | D. | $2\sqrt{2}$ |
15.已知P(t,3t),t∈R,M是圆O1:(x+2)2+y2=$\frac{1}{4}$上的动点,N是O2:(x-4)2+y2=$\frac{1}{4}$上的动点,则|PN|-|PM|的最大值是( )
| A. | $\frac{3\sqrt{5}}{5}$+1 | B. | $\frac{3\sqrt{5}}{5}-1$ | C. | $\frac{6\sqrt{5}}{5}$+1 | D. | $\frac{6\sqrt{5}}{5}$ |
19.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”,在下面的六个点M(1,1)、N(1,2)、P(1,3)、Q(2,1)、R(2,2)、T(2,3)中,“好点”的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.下列函数中,在区间(0,+∞)上为减函数的是( )
| A. | y=x+1 | B. | y=$\sqrt{x+1}$ | C. | y=($\frac{1}{2}$)x | D. | y=-$\frac{1}{x}$ |