题目内容
12．已知在极坐标下曲线C：ρ（cosθ+2sinθ）=4与点A（2，$\frac{π}{3}$），求曲线C与点A的位置关系．分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出直角坐标方程，把点A的直角坐标代入即可判断出位置关系．
解答 解：曲线C：ρ（cosθ+2sinθ）=4化为x+2y=4，
点A（2，$\frac{π}{3}$），化为直角坐标为$A（2cos\frac{π}{3}，2sin\frac{π}{3}）$，即A$（1，\sqrt{3}）$，
∵1+2$\sqrt{3}$≠4，
∴点A不在曲线C上．
点评 本题考查了极坐标方程化为直角坐标方程的方法、点与直线的位置关系，考查了计算能力，属于基础题．
练习册系列答案
相关题目
2．已知函数f（x）=x2+3x-21nx，则函数f（x）的单调递减区间为（ ）
| A． | （-2，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，+∞] | C． | （-∞，-2） | D． | （0，$\frac{1}{2}$） |
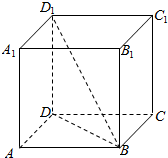在正方体ABCD-A1B1C1D1中，对角线BD1分别与平面AC，平面BC1，平面BA1所成的角，并求这些角的余弦值．
已知直线AC与圆O相切于点B，AD交圆O于F，D两点，CF交圆O于E，F两点，BD∥CE，AB=BC，AD=2，BD=1，则CE=4．