题目内容
已知命题p:函数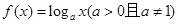 在区间(0,+∞)上单调递增,命题q:函数f(x)=ax2-ax+1对于任意x∈R都有f(x)>0恒成立.如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
在区间(0,+∞)上单调递增,命题q:函数f(x)=ax2-ax+1对于任意x∈R都有f(x)>0恒成立.如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
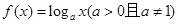 在区间(0,+∞)上单调递增,命题q:函数f(x)=ax2-ax+1对于任意x∈R都有f(x)>0恒成立.如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
在区间(0,+∞)上单调递增,命题q:函数f(x)=ax2-ax+1对于任意x∈R都有f(x)>0恒成立.如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.(0,1)∪[4,+∞)。
试题分析:若命题p为真,有a>1.所以p为假时,0<a<1 2分
若命题q为真,有a=0或
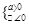 即a=0或
即a=0或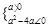 ⇒0≤a<4.
⇒0≤a<4.所以命题q为假时,a<0或a≥4. 4分
因为p∨q为真命题,p∧q为假命题,
所以p,q有且只有一个是真命题,即p,q一真一假. 6分
所以有p真q假或p假q真.
所以
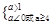 或
或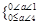 ⇒a≥4或0<a<1. 10分
⇒a≥4或0<a<1. 10分所以所求a的取值范围是(0,1)∪[4,+∞). 12分
点评:本题以复合命题的真假判断为载体,主要考查了对数函数的单调性和二次函数恒成立问题,应当熟练掌握.做本题时,别忘记讨论二次项系数为0的情况。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
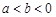 ”是“
”是“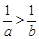 ”的( )条件
”的( )条件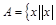 ≤3,
≤3, ,
,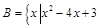 ≤0,
≤0, ”是“
”是“ ”的充分条件但不是必要条件
”的充分条件但不是必要条件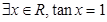 ;命题q:
;命题q: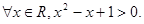
 ”是假命题;
”是假命题;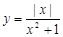 的最小值为
的最小值为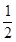 且它的图像关于y轴对称;
且它的图像关于y轴对称; ③“
③“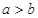 ”是“
”是“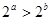 ”的充分不必要条件;
”的充分不必要条件;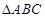 中,若
中,若 ,则
,则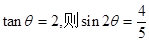 ;
;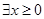 ,
,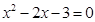 ”的否定是 .
”的否定是 .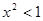 ,则
,则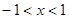 ”的逆否命题为__ _____
”的逆否命题为__ _____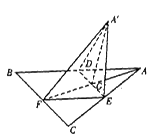
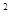 =4的解是x=±2”中,逻辑联结词的使用情况是( )
=4的解是x=±2”中,逻辑联结词的使用情况是( )