题目内容
4.在等差数列{an}中,a3+a4+a5=21,a9=17.(1)求数列{an}的通项公式;
(2)令bn=2an-an(n∈N*),求数列{bn}的前n项和Sn.
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式,解方程可得首项和公差,即可得到所求通项;
(2)求得bn=2an-an=22n-1-(2n-1),运用数列的求和方法:分组求和,借助等差数列和等比数列的求和公式,计算即可得到所求.
解答 解:(1)设等差数列{an}的公差为d,
由a3+a4+a5=21,a9=17,
即为3a1+9d=21,a1+8d=17,
解得a1=1,d=2,所以an=2n-1;
(2)bn=2an-an=22n-1-(2n-1),
数列{bn}的前n项和Sn=(2-1)+(23-3)+…+(22n-1-(2n-1))
=(2+23+…+22n-1)-(1+3+…+2n-1)
=$\frac{2(1-{4}^{n})}{1-4}$-$\frac{1}{2}$(1+2n-1)n=$\frac{2({4}^{n}-1)}{3}$-n2.
点评 本题考查等差数列的通项公式和求和公式的运用,同时考查数列的求和方法:分组求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
9.已知圆C1:x2+y2-4x-4y-1=0,圆C2:x2+y2+2x+8y-8=0,圆C1与圆C2的位置关系为( )
| A. | 外切 | B. | 相离 | C. | 相交 | D. | 内切 |
14.关于x的方程${({\frac{2}{3}})^x}=\frac{1+a}{1-a}$有负实数根,则a的取值范围是( )
| A. | (-1,1) | B. | (0,1) | C. | (-1,0) | D. | $({-\frac{2}{3},\frac{2}{3}})$ |
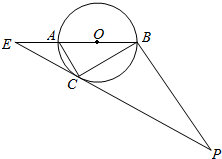 如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.
如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.