题目内容
16.已知函数f(x)=2x3+ax2+2在x=1时取得极值.(1)求a;
(2)求f(x)在$[-\frac{1}{2},2]$上的最值.
分析 (1)利用函数的导数,通过函数的极值点,求解即可.
(2)求出函数的极值点,判断函数的单调性,然后求解最值.
解答 (本题满分12分)
解:(1)f′(x)=6x2+2ax,由题意得f′(1)=0⇒a=-3;
(2)由(1)f′(x)=6x(x-1),令f′(x)=0⇒x=0或x=1
当x变化时,f′(x),f(x)的变化情况如下表:
| x | $(-\frac{1}{2},0)$ | 0 | (0,1) | 1 | (1,2) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 2 | ↘ | 1 | ↗ |
所以fmax(x)=6,fmin(x)=1
点评 本题考查函数的极值点以及函数的单调性的应用,函数的最值的求法,考查计算能力.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
1.定义在实数集R上的函数y=f(x)满足$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$>0(x1≠x2),若f(5)=-1,f(7)=0,那么f(-3)的值可以为( )
| A. | 5 | B. | -5 | C. | 0 | D. | -1 |
5.$\sqrt{5}+1$与$\sqrt{5}-1$两数的等比中项是(
| A. | 2 | B. | -2 | C. | ±2 | D. | 以上均不是 |
6.若变量y与x之间的相关系数r=-0.9362,查表得到相关系数临界值r0.05=0.8013,则变量y与x之间( )
| A. | 不具有线性相关关系 | B. | 具有线性相关关系 | ||
| C. | 它们的线性关系还要进一步确定 | D. | 不确定 |
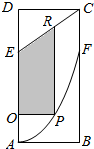 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.