题目内容
【题目】不期而至的新冠肺炎疫情，牵动了亿万国人的心，全国各地纷纷捐赠物资驰援武汉.有一批捐赠物资需要通过轮船沿长江运送至武汉，已知该运送物资的轮船在航行中每小时的燃料费和它的速度的立方成正比，已知当速度为10海里/时时，燃料费是6元/时，而其他与速度无关的费用是96元/时，问当轮船的速度是多少时，航行1海里所需的费用总和最小？
【答案】当轮船的速度为20海里/时时，航行1海里所需费用总和最小.
【解析】
设速度为
海里/时的燃料费是p元/时，由题设的比例关系得
，由数据可得
，列出航行1海里的总费用为
，再利用导数求出最值即可.
设速度为海里/时的燃料费是p元/时，
由题设的比例关系得，其中k为比例系数.
由
，
，得
，
于是.
设船的速度为海里/时，航行1海里所需的总费用为y元，
而每小时所需的总费用是
元，航行1海里所需时间为
，
所以航行1海里的总费用为
.
所以
.
令
，解得
.
因为当
时，
；当
时，
，
所以当时，y取得最小值.
故当轮船的速度为20海里/时时，航行1海里所需费用总和最小.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
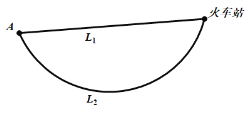
【题目】如图，
地到火车站共有两条路径，据统计两条路径所用的时间互不影响，所用时间在各时间段内的的频率如下表：
时间（分钟） |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
现甲、乙两人分别有
分钟和
分钟时间用于赶往火车站.
（1）为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
（2）用
表示甲、乙两人中在允许的时间内赶到火车站的人数，针对（1）的选择方案，求的分布列和数学期望.
