题目内容
【题目】设直线与函数![]() 的图像恰有两个不同的公共点.求出所有这样的直线方程.
的图像恰有两个不同的公共点.求出所有这样的直线方程.
【答案】![]()
【解析】
显然,直线![]() 与函数
与函数![]() 的图像只有一个公共点.于是,
的图像只有一个公共点.于是,
设直线方程为![]() .将其代入
.将其代入![]() ,
,
得![]() . ①
. ①
方程①恰有两个不同实根,有如下3种情形:
(1)![]() ,
,
其中,![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,且
,且![]() .
.
(2)![]() ,其中,
,其中,![]() 、
、![]() ,且
,且![]() .
.
(3)![]() ,其中,
,其中,![]() 、
、![]() ,且
,且![]() .
.
对于(1),可设![]() ,
,
其中,![]() ,
,![]() .
.
展开比较系数得![]() ,
,![]() ,
,![]() ,
,![]() .
.
由前两个方程得![]() ,
,![]() ,代入
,代入![]() ,
,![]() ,得
,得
![]() .
.
所以,![]() .
.
故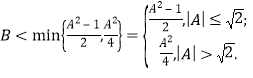
则![]() ,
,![]() .
.
直线方程为![]() ,
,
其中,实数![]() 、
、![]() 满足
满足![]() .
.
比如,取![]() ,则
,则![]() ;取
;取![]() ,则
,则![]() ,
,![]() .因此,直线方程为
.因此,直线方程为![]() .
.
此时,方程①为![]() .
.
对于(2),可设![]() ,其中,
,其中,![]() .
.
在(1)的方程组中令![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,![]() .
.
解得![]() ,
,![]() ,
,![]() ,
,![]() .
.
因此,直线方程为![]() .
.
对于(3),展开比较系数得![]() ,
,![]() ,
,![]() ,
,![]() .
.
由前两个方程得![]() ,
,![]() .解得
.解得![]() .
.
注意到,![]() ,
,![]() ,
,
于是,![]() .
.
此时,直线方程为![]() .
.

练习册系列答案
相关题目
【题目】已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
| 3 |
| 4 |
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.

