题目内容
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.若
的左、右焦点.若![]() 是该椭圆上的一个动点,
是该椭圆上的一个动点,![]() 的最大值为1.
的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与
与![]() 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(1)由题意可得![]() ,
,![]() ,设
,设![]() ,根据
,根据![]() 的最大值可得
的最大值可得![]() ,从而得到椭圆的方程.(2)将直线方程代入椭圆方程消去x后得到关于
,从而得到椭圆的方程.(2)将直线方程代入椭圆方程消去x后得到关于![]() 的二次方程,设
的二次方程,设![]() ,
,![]() ,则
,则![]() ,则可得经过点
,则可得经过点![]() 的直线方和为
的直线方和为![]() ,令
,令![]() ,结合根与系数的关系可得
,结合根与系数的关系可得![]() ,从而可得直线
,从而可得直线![]() 与
与![]() 轴交于定点
轴交于定点![]() .
.
详解:(1)由题意得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设![]() ,则
,则![]()
![]() ,
,
∵![]() ,
,
∴当![]() ,即点
,即点![]() 为椭圆长轴端点时,
为椭圆长轴端点时,![]() 有最大值1,
有最大值1,
即![]() ,解得
,解得![]() ,
,
故所求的椭圆方程为![]() .
.
(2)由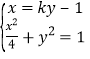 得消去x整理得
得消去x整理得![]() ,
,
显然![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
故![]() ,
,![]() .
.
∴经过点![]() ,
,![]() 的直线方和为
的直线方和为![]() ,
,
令![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,
,
∴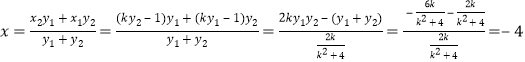 ,
,
即当![]() .
.
∴直线![]() 与
与![]() 轴交于定点
轴交于定点![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目