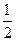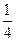题目内容
(本小题满分10分)
用平行于四面体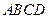 的一组对棱
的一组对棱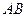 、
、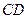 的平面截此四面体(如图).
的平面截此四面体(如图).
(1)求证:所得截面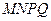 是平行四边形;
是平行四边形;
(2)如果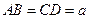 .求证:四边形
.求证:四边形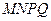 的周长为定值.
的周长为定值.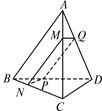
用平行于四面体
 的一组对棱
的一组对棱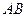 、
、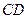 的平面截此四面体(如图).
的平面截此四面体(如图).
(1)求证:所得截面
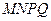 是平行四边形;
是平行四边形;(2)如果
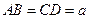 .求证:四边形
.求证:四边形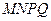 的周长为定值.
的周长为定值.
解:(1)∵AB∥平面MNPQ.
平面ABC∩平面MNPQ=MN.
且AB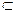 平面ABC.
平面ABC.
∴由线面平行的性质定理知,AB∥MN.
同理可得PQ∥AB. …………3分
∴由平行公理可知MN∥PQ.
同理可得MQ∥NP.
∴截面四边形MNPQ为平行四边形. …………5分
…………5分
(2)∵由(1)可知MN∥AB.∴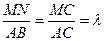 .
.
∵MN=λAB=λa,MC=λAC. …………7分
又∵MG∥CD,∴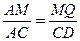 .
.
∴MQ=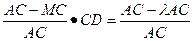 ·CD=(1-λ)a, …………9分
·CD=(1-λ)a, …………9分
∴MN+MQ=λa+(1-λ)a=a.
∴平行四边形MNPQ的周长2(MN+MQ)=2a定值. …………10分
平面ABC∩平面MNPQ=MN.
且AB
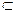 平面ABC.
平面ABC.∴由线面平行的性质定理知,AB∥MN.
同理可得PQ∥AB. …………3分
∴由平行公理可知MN∥PQ.
同理可得MQ∥NP.
∴截面四边形MNPQ为平行四边形.
 …………5分
…………5分(2)∵由(1)可知MN∥AB.∴
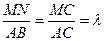 .
.∵MN=λAB=λa,MC=λAC. …………7分
又∵MG∥CD,∴
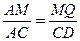 .
.∴MQ=
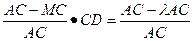 ·CD=(1-λ)a, …………9分
·CD=(1-λ)a, …………9分∴MN+MQ=λa+(1-λ)a=a.
∴平行四边形MNPQ的周长2(MN+MQ)=2a定值. …………10分
略

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 -ABC的底面是边长为2的正三角形,顶点
-ABC的底面是边长为2的正三角形,顶点 在底面上的射影是△ABC的中心,
在底面上的射影是△ABC的中心, 与AB的夹角是45°
与AB的夹角是45°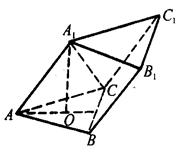
 1)求证:
1)求证: ⊥平面
⊥平面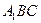 ;
;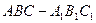 的所有棱长都为4,
的所有棱长都为4,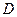 为
为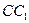 的中点.
的中点.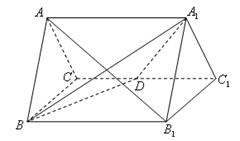
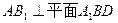 ;
;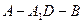 的大小.
的大小.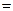 a,AD
a,AD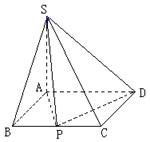
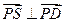 .
. 个单位法向量
个单位法向量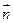
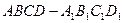 的底面为正方形,
的底面为正方形,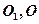 分别为上、下底面的中心,且
分别为上、下底面的中心,且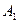 在底面
在底面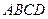 的射影是
的射影是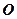 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面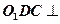 平面
平面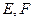 分别在棱上
分别在棱上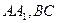 上,且
上,且 ,问点
,问点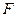 在何处时,
在何处时,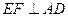 ;
;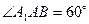 ,求二面角
,求二面角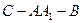 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。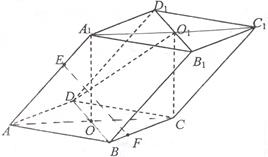
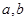 分别在平面
分别在平面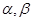 内,且平面
内,且平面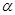 与
与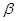 的交线为
的交线为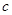 ,则直线
,则直线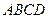 是边长为
是边长为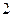 的正方形,
的正方形,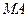 和
和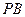 都与平面
都与平面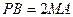
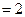 ,设平面
,设平面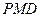 与平面
与平面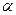 ,则
,则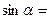 ▲
▲ 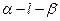 的大小是60°,线段
的大小是60°,线段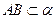 .
.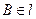 ,
,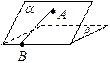
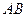 与
与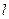 所成的角为30°.则
所成的角为30°.则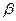 所成的角的正弦值是▲
所成的角的正弦值是▲  梯形ABCD中,
梯形ABCD中,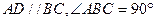 ,
, E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.
E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.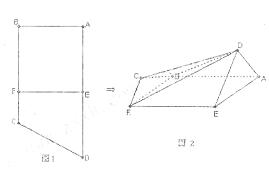
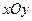 中,已知平面区域
中,已知平面区域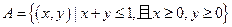 ,则平面区域
,则平面区域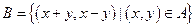 的面积为( )
的面积为( )