题目内容
已知椭圆方程为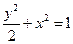 ,斜率为
,斜率为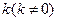 的直线
的直线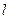 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于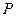 ,
,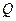 两点,线段
两点,线段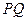 的垂直平分线与
的垂直平分线与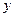 轴相交于点
轴相交于点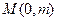 .
.
(Ⅰ)求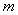 的取值范围;
的取值范围;
(Ⅱ)求△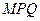 面积的最大值.
面积的最大值.
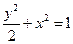 ,斜率为
,斜率为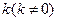 的直线
的直线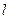 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于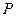 ,
,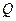 两点,线段
两点,线段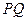 的垂直平分线与
的垂直平分线与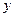 轴相交于点
轴相交于点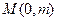 .
.(Ⅰ)求
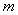 的取值范围;
的取值范围;(Ⅱ)求△
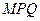 面积的最大值.
面积的最大值.(Ⅰ)设直线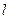 的方程为
的方程为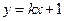 ,由
,由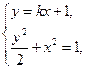 可得
可得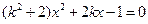 .
.
设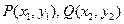 ,则
,则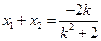 ,
,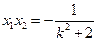 .
.
可得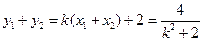 .……………………………3分
.……………………………3分
设线段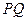 中点为
中点为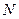 ,则点
,则点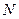 的坐标为
的坐标为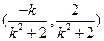 ,
,
由题意有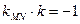 ,可得
,可得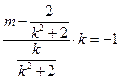 .可得
.可得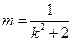 ,
,
又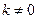 ,所以
,所以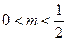 .……………………6分
.……………………6分
(Ⅱ)设椭圆上焦点为 ,则
,则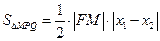
 ………………9分
………………9分
所以△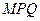 的面积为
的面积为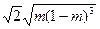 (
(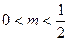 ).
).
设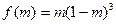 ,则
,则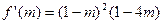 .
.
可知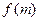 在区间
在区间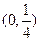 单调递增,在区间
单调递增,在区间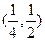 单调递减.
单调递减.
所以,当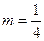 时,
时,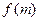 有最大值
有最大值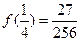 .
.
所以,当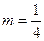 时,△
时,△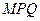 的面积有最大值
的面积有最大值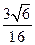 .……………12分
.……………12分
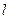 的方程为
的方程为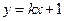 ,由
,由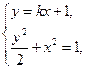 可得
可得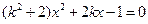 .
.设
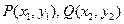 ,则
,则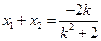 ,
,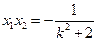 .
.可得
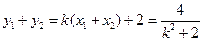 .……………………………3分
.……………………………3分设线段
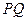 中点为
中点为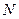 ,则点
,则点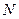 的坐标为
的坐标为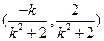 ,
,由题意有
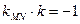 ,可得
,可得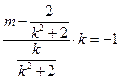 .可得
.可得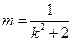 ,
,又
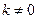 ,所以
,所以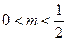 .……………………6分
.……………………6分(Ⅱ)设椭圆上焦点为
 ,则
,则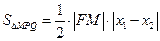
 ………………9分
………………9分所以△
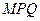 的面积为
的面积为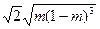 (
(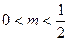 ).
).设
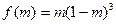 ,则
,则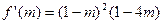 .
.可知
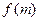 在区间
在区间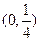 单调递增,在区间
单调递增,在区间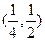 单调递减.
单调递减.所以,当
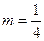 时,
时,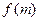 有最大值
有最大值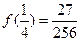 .
.所以,当
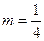 时,△
时,△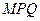 的面积有最大值
的面积有最大值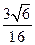 .……………12分
.……………12分略

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
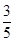 或
或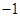
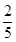
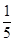 或
或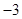
 是椭圆
是椭圆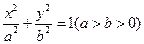 的左、右焦点,过点
的左、右焦点,过点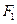 作
作 的直线
的直线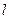 交椭圆于
交椭圆于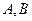 两点,
两点,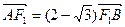 .
.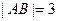 ,求椭圆的标准方程.
,求椭圆的标准方程.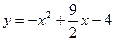 ,过原点O作抛物线C的切线
,过原点O作抛物线C的切线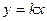 使切点P在第一象限,
使切点P在第一象限,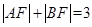 ,则线
,则线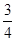
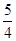
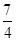
 的焦点在
的焦点在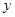 轴上,
轴上, ,
, ,则这样的椭圆个数共有 ( )
,则这样的椭圆个数共有 ( ) 、
、
 、
、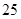
 、
、
 、
、
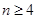 ,
,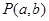 是平面直角坐标系
是平面直角坐标系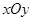 中的点,其中
中的点,其中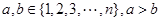
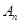 为满足
为满足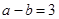 的点
的点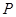 的个数,求
的个数,求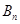 为满足
为满足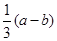 是整数的点
是整数的点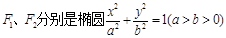 的左、右焦点,
的左、右焦点,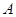 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点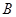 也在椭圆 上,且满足
也在椭圆 上,且满足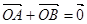 (
(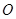 为坐标原点),
为坐标原点),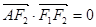 ,若椭圆的离心率等于
,若椭圆的离心率等于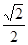 , 则直线
, 则直线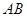 的方程是 ( ▲ ) .
的方程是 ( ▲ ) .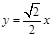
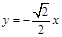
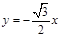
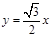
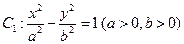 的左、右焦点分别为
的左、右焦点分别为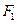 、
、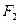 ,抛物线
,抛物线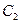 的顶点在原点,它的准线与双曲线
的顶点在原点,它的准线与双曲线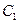 的左准线重合,若双曲线
的左准线重合,若双曲线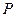 满足
满足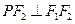 ,则双曲线
,则双曲线