题目内容
将边长为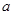 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
小正方形的边长为,容积最大为
解析试题分析:设小正方形的边长为x,则盒底的边长为a-2x,
∴方盒的体积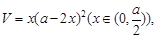 ……………………………………4分
……………………………………4分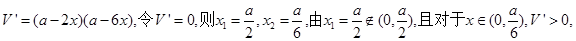
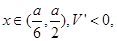 ……………………………………10分
……………………………………10分
∴函数V在点x=处取得极大值,由于问题的最大值存在,
∴V()=即为容积的最大值,此时小正方形的边长为.…………………12分
考点:函数导数求解实际问题
点评:将实际问题转化为单存的数学问题时要注意自变量x的取值范围,本题首先找到边长与容积的关系式,通过导数即可求其最大值

练习册系列答案
相关题目
 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上,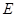 在
在 上.
上.
 ,求用
,求用 表示
表示 的函数关系式;
的函数关系式; m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
 。
。 上的单调性并加以证明;
上的单调性并加以证明; 的值域是(1,+
的值域是(1,+ ),求a的值。
),求a的值。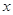 元.
元.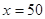 时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)
时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)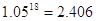 ,
,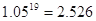 ,
,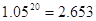 ,
, 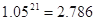 )
) ,在
,在 时取得极值.
时取得极值. 的解析式;
的解析式; 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.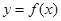 的图象.写出
的图象.写出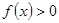 的解集;
的解集;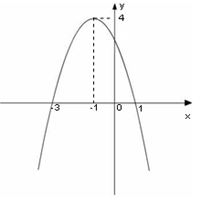
 在何范围内变化时,
在何范围内变化时,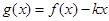 在区间
在区间 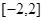 上是单调函数.
上是单调函数.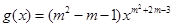 是幂函数且在
是幂函数且在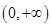 上为减函数,函数
上为减函数,函数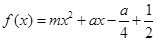 在区间
在区间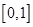 上的最大值为2,试求实数
上的最大值为2,试求实数 的值。
的值。