题目内容
建造一断面为等腰梯形的防洪堤(如图),梯形的腰与底边所角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
上面宽BC=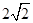 m时,断面的外周长最小,水泥用料最省
m时,断面的外周长最小,水泥用料最省
解析试题分析:如图,自B作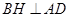 于H.
于H.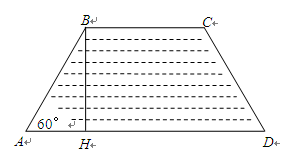
设AH = x,断面的外周长为y.
在Rt△AHB中,因为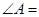 60°,
60°,
所以AB = 2x,BH = 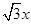 .
.
于是梯形ABCD的面积S =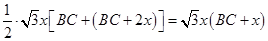 ,
,
所以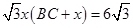 ,解得
,解得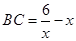 . 6分
. 6分
由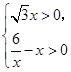 解得
解得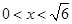 . 8分
. 8分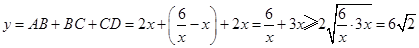 ,
,
当且仅当 即
即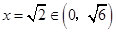 时取“=”号. 14分
时取“=”号. 14分
故当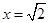 m即上面宽BC=
m即上面宽BC=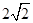 m时,断面的外周长最小,水泥用料最省.…16分
m时,断面的外周长最小,水泥用料最省.…16分
考点:函数应用题
点评:求解本题的关键在于首先找到面积与一边长的函数关系式,但要结合实际问题注意函数的定义域在实际问题中的限定条件

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

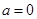 ,解不等式
,解不等式 ;
;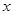 的不等式
的不等式
 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, .
. 的解析式;
的解析式;  ,求函数
,求函数 的最小值.
的最小值. 的图像顶点为
的图像顶点为 ,且图像在x轴上截得线段长为8
,且图像在x轴上截得线段长为8
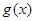 在
在 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围;
的取值范围;  层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层? 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
 ,画出函数
,画出函数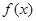 的图像,并求出函数
的图像,并求出函数 的零点;
的零点; ,且对任意
,且对任意 ,
,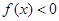 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.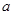 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少? 若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和. (其中
(其中 为大于0的常数),在
为大于0的常数),在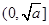 上是减函数,在
上是减函数,在 上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.  .已知甲、乙两地相距100千米。
.已知甲、乙两地相距100千米。