题目内容
19.在△ABC中,b=1,c=$\sqrt{3}$,B=30°,则C的大小为( )| A. | 30° | B. | 30°或150° | C. | 60°或120° | D. | 60° |
分析 利用已知及正弦定理即可求得sinC=$\frac{\sqrt{3}}{2}$,结合C的范围即可得解.
解答 解:∵由正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}=2$,
∴解得:sinC=$\frac{\sqrt{3}}{2}$,
∴解得:C=60°或120°.
故选:C.
点评 本题主要考查了正弦定理的应用,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
10.某高校“统计初步”课程教师随机调查了选该课的一些学生情况,共调查了50人,其中女生27人,男生23人,女生中有20人选统计专业,另外7人选非统计专业;男生中有10人选统计专业,另外13人选非统计专业.
(Ⅰ)根据以上数据完成下列2×2列联表:
(Ⅱ)根据以上数据,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系?
参考数据:附:X2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当X2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当X2>2.706时,有90%的把握判定变量A,B有关联;
当X2>3.814时,有95%的把握判定变量A,B有关联;
当X2>6.635时,有99%的把握判定变量A,B有关联.
(Ⅰ)根据以上数据完成下列2×2列联表:
| 专业 性别 | 非统计专业 | 统计专业 | 总计 |
| 男 | |||
| 女 | |||
| 总计 |
参考数据:附:X2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当X2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当X2>2.706时,有90%的把握判定变量A,B有关联;
当X2>3.814时,有95%的把握判定变量A,B有关联;
当X2>6.635时,有99%的把握判定变量A,B有关联.
14.下列各函数中,最小值为2的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$ | D. | y=5x+5-x |
10.已知△ABC中,a=2$\sqrt{2}$,b=2$\sqrt{3}$,B=60°,那么角sinA等于( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
 是偶函数,且当
是偶函数,且当 时,
时,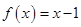 ,则不等式
,则不等式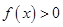 的解集是( )
的解集是( )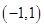 B.
B.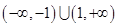
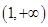 D.
D.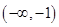
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 ,
, ,
, ,且满足
,且满足 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.