题目内容
【题目】已知函数f(x)=sin(ωx+φ)(其中ω>0|φ|< ![]() )图象相邻对称轴的距离为
)图象相邻对称轴的距离为 ![]() ,一个对称中心为(﹣
,一个对称中心为(﹣ ![]() ,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
【答案】D
【解析】解:由题意可得函数的最小正周期为 ![]() =2×
=2× ![]() ,∴ω=2.
,∴ω=2.
再根据﹣ ![]() ×2+φ=kπ,|φ|<
×2+φ=kπ,|φ|< ![]() ,k∈z,可得φ=
,k∈z,可得φ= ![]() ,f(x)=sin(2x+
,f(x)=sin(2x+ ![]() ),
),
故将f(x)的图象向左平移 ![]() 个单位,可得y=sin[2(x+
个单位,可得y=sin[2(x+ ![]() )+
)+ ![]() ]=sin(2x+
]=sin(2x+ ![]() )=cos2x的图象,
)=cos2x的图象,
故选:D.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

【题目】“北祠堂”是我校著名的一支学生乐队,对于2015年我校“校园周末文艺广场”活动中“北祠堂”乐队的表现,在高一年级学生中投票情况的统计结果见表:
喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
人数 | 500 | 200 | 100 |
现采用分层抽样的方法从所有参与对“北祠堂”投票的800名学生中抽取一个容量为n的样本,若从不喜欢“北祠堂”的100名学生中抽取的人数是5人.
(1)求n的值;
(2)若从不喜欢“北祠堂”的学生中抽取的5人中恰有3名男生(记为a1 , a2 , a3)2名女生(记为b1 , b2),现将此5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.
【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生. 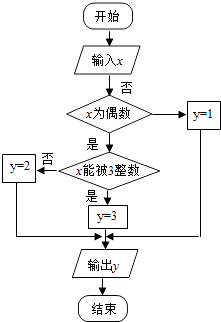
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.