题目内容
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,若点
,若点![]() 为抛物线
为抛物线![]() 准线上的动点,给出以下命题:
准线上的动点,给出以下命题:
①当![]() 为正三角形时,
为正三角形时,![]() 的值为
的值为![]() ;
;
②存在![]() 点,使得
点,使得![]() ;
;
③若![]() ,则
,则![]() 等于
等于![]() ;
;
④![]() 的最小值为
的最小值为![]() ,则
,则![]() 等于
等于![]() 或
或![]() .
.
其中正确的是( )
A.①③④B.②③C.①③D.②③④
【答案】A
【解析】
对于①可知,当![]() 为正三角形时
为正三角形时![]() 与准线垂直,画出图形结合几何关系即可求得
与准线垂直,画出图形结合几何关系即可求得![]() 的值;对于②根据向量关系可知
的值;对于②根据向量关系可知![]() ,结合点的位置即可判断;对于③,作出几何图形,根据线段比例关系即可求得
,结合点的位置即可判断;对于③,作出几何图形,根据线段比例关系即可求得![]() 的值;对于④,作
的值;对于④,作![]() 关于准线的对称点
关于准线的对称点![]() ,连接
,连接![]() 交准线于
交准线于![]() ,可知
,可知![]() 即为
即为![]() 的最小值,根据线段几何关系及最小值即可求得
的最小值,根据线段几何关系及最小值即可求得![]() 的值.
的值.
对于①,当![]() 为正三角形时,如下图所示,
为正三角形时,如下图所示,
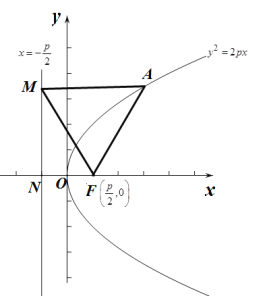
抛物线的准线交![]() 轴于
轴于![]() ,
,
![]() ,由抛物线定义可知
,由抛物线定义可知![]() ,则
,则![]() 与准线垂直,
与准线垂直,
所以![]() ,
,
则![]() ,所以
,所以![]() ,
,
而![]() ,即
,即![]() ,所以①正确;
,所以①正确;
对于②,假设存在![]() 点,使得
点,使得![]() ,即
,即![]() ,
,
所以![]() 点为
点为![]() 的中点,
的中点,
由抛物线图像与性质可知,![]() 为抛物线上一点,
为抛物线上一点,![]() 为焦点,线段
为焦点,线段![]() 在
在![]() 轴右侧,
轴右侧,
点![]() 在抛物线
在抛物线![]() 准线上,在
准线上,在![]() 轴左侧,因而
轴左侧,因而![]() 不可能为
不可能为![]() 的中点,所以②错误;
的中点,所以②错误;
对于③,若![]() ,则
,则![]() ,作
,作![]() 垂直于准线并交于
垂直于准线并交于![]() ,准线交
,准线交![]() 轴于
轴于![]() ,如下图所示:
,如下图所示:
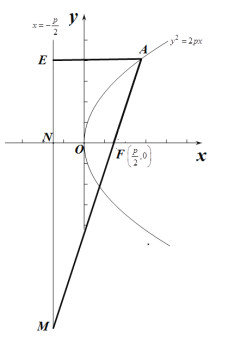
由抛物线定义可知![]() ,
,
根据相似三角形中对应线段成比例可知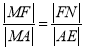 ,即
,即![]() ,
,
解得![]() ,所以③正确;
,所以③正确;
对于④,作![]() 关于准线的对称点
关于准线的对称点![]() ,连接
,连接![]() 交准线于
交准线于![]() ,作
,作![]() 垂直于准线并交于
垂直于准线并交于![]() ,作
,作![]() 垂直于
垂直于![]() 轴并交于
轴并交于![]() ,如下图所示:
,如下图所示:
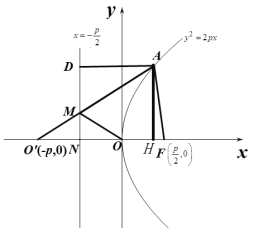
根据对称性可知,此时![]() 即为
即为![]() 的最小值,
的最小值,
由抛物线定义可知![]() ,所以
,所以![]() 的横坐标为
的横坐标为![]() ,
,
代入抛物线可知![]() ,
,
![]() 的最小值为
的最小值为![]() ,
,![]() ,
,
则![]() ,即
,即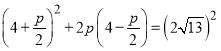 ,
,
化简可得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,所以④正确;
,所以④正确;
综上所述,正确的为①③④.
故选:A.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: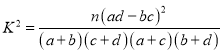 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为了比较两种治疗失眠症的药(分别称为![]() 药,
药,![]() 药)的疗效,某机构随机地选取
药)的疗效,某机构随机地选取![]() 位患者服用
位患者服用![]() 药,
药,![]() 位患者服用
位患者服用![]() 药,观察这
药,观察这![]() 位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:
位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:![]() ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
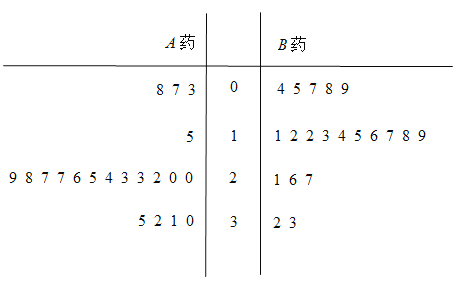
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这![]() 名患者日平均增加睡眠时间的中位数
名患者日平均增加睡眠时间的中位数![]() ,并将日平均增加睡眠时间超过
,并将日平均增加睡眠时间超过![]() 和不超过
和不超过![]() 的患者人数填入下面的列联表:
的患者人数填入下面的列联表:
超过 | 不超过 | |
服用 | ||
服用 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 两种药的疗效有差异?
两种药的疗效有差异?
附: 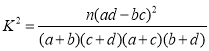 .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |