题目内容
已知等差数列{an}的前5项和为105,且a10=2a5.
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中不大于72m的项的个数记为bm,求数列{bm}的前m项和Sm.
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中不大于72m的项的个数记为bm,求数列{bm}的前m项和Sm.
(1) an=7n(n∈N*) (2)Sm=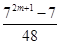
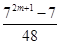
解:(1)设数列{an}的公差为d,前n项和为Tn,
∵T5=105,a10=2a5,
∴
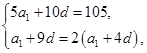
解得a1=7,d=7,
∴an=7+(n-1)·7=7n(n∈N*).
(2)对m∈N*由an=7n≤72m,
得n≤72m-1,
即bm=72m-1=7·49m-1
∴数列{bm}是首项为7,公比为49的等比数列,
∴Sm=
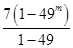 =
=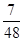 (49m-1)=
(49m-1)=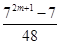 .
.
练习册系列答案
相关题目
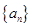 的首项为
的首项为 ,公差为
,公差为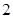 ,数列
,数列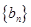 满足
满足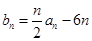 ,
,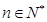 .
.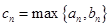 ,求数列
,求数列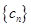 的前
的前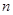 项和
项和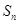 .
.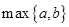 表示
表示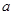 与
与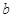 的最大值.)
的最大值.)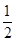 .
.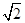 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.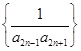 的前n项和.
的前n项和.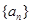 中,
中,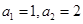 ,设
,设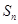 为数列
为数列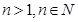 ,
,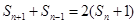 都成立,则
都成立,则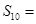 .
.