题目内容
【题目】二次函数f(x),又 ![]() 的图象与x轴有且仅有一个公共点,且f′(x)=1﹣2x.
的图象与x轴有且仅有一个公共点,且f′(x)=1﹣2x.
(1)求f(x)的表达式.
(2)若直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,求k的值.
【答案】
(1)解:设f(x)=ax2+bx+c,则f′(x)=2ax+b,
∵f′(x)=1﹣2x,∴a=﹣1,b=1,
∴ ![]() =
= ![]() 的图象与x轴有且仅有一个公共点,
的图象与x轴有且仅有一个公共点,
∴△=1+4(c﹣ ![]() )=0,解得c=0,
)=0,解得c=0,
则f(x)=x﹣x2
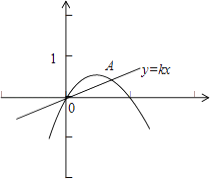
(2)解:由(1)得f(x)=x﹣x2图象与x轴交点是(0,0)、(1,0),
如图:直线y=kx和y=f(x)的图象的交点为A,
由 ![]() 得,x=1﹣k,
得,x=1﹣k,
∵直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,
∴ ![]() dx=
dx= ![]() ,
,
即 ![]() ×(
×( ![]() )=
)= ![]() ,
,
![]() ,解得
,解得 ![]() ,
,
故k的值是 ![]() .
.
【解析】(1)由题意设f(x)=ax2+bx+c,求出f′(x)后结合题意求出a、b,再代入 ![]() 化简,由题意和二次函数的性质令△=0求出c的值,代入解析式求出f(x);(2)先求出f(x)=x﹣x2图象与x轴交点坐标,再画出图象,并求出y=kx和y=f(x)的图象的交点的横坐标,结合题意和定积分知识列出方程,求出k的值.
化简,由题意和二次函数的性质令△=0求出c的值,代入解析式求出f(x);(2)先求出f(x)=x﹣x2图象与x轴交点坐标,再画出图象,并求出y=kx和y=f(x)的图象的交点的横坐标,结合题意和定积分知识列出方程,求出k的值.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).

练习册系列答案
相关题目