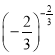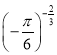题目内容
【题目】设[x]表示不超过x的最大整数,如:[π]=3,[﹣4.3]=﹣5.给出下列命题: ①对任意实数x,都有[x]﹣x≤0;
②若x1≤x2 , 则[x1]≤[x2];
③[lg1]+[lg2]+[lg3]+…+[lg100]=90;
④若函数f(x)= ![]() ﹣
﹣ ![]() ,则y=[f(x)]+[f(﹣x)]的值域为{﹣1,0}.
,则y=[f(x)]+[f(﹣x)]的值域为{﹣1,0}.
其中所有真命题的序号是 .
【答案】①②④
【解析】解:对于①,对任意实数x,都有[x]﹣x≤0,满足新定义∴①正确.
对于②,x1≤x2,则[x1]≤[x2],∴②正确.
对于③,[lg1]+[lg2]+[lg3]+[lg4]+…+[lg100]
=0+1×90+2=92,∴③不正确.
对于④,函数f(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
同理可得,f(﹣x)∈(﹣ ![]() ,
, ![]() ),
),
当f(x)∈ ![]() 时,f(﹣x)∈(0,
时,f(﹣x)∈(0, ![]() ),∴[f(x)]=﹣1,[f(﹣x)]=0,
),∴[f(x)]=﹣1,[f(﹣x)]=0,
∴[f(x)]+[f(﹣x)]=﹣1,
同理当f(﹣x)∈ ![]() 时,f(x)∈(0,
时,f(x)∈(0, ![]() ),∴[f(x)]=0,[f(﹣x)]=﹣1,
),∴[f(x)]=0,[f(﹣x)]=﹣1,
∴[f(x)]+[f(﹣x)]=﹣1,
当f(x)=0时,f(﹣x)=0,∴[f(x)]=0,[f(﹣x)]=0,
∴[f(x)]+[f(﹣x)]=0,
综上,y=[f(x)]+[f(﹣x)]={﹣1,0}
∴④正确.
所以答案是:①②④.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表: A型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
( I)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.