题目内容
已知等差数列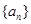 的首项
的首项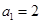 ,
,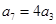 ,前
,前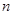 项和为
项和为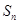 .
.
(I)求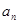 及
及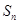 ;
;
(Ⅱ)设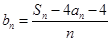 ,
,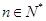 ,求
,求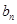 的最大值.
的最大值.
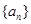 的首项
的首项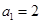 ,
,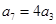 ,前
,前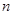 项和为
项和为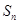 .
.(I)求
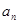 及
及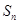 ;
;(Ⅱ)设
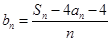 ,
,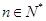 ,求
,求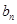 的最大值.
的最大值.(1)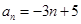 ,
,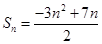 ;(2)
;(2)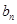 的最大值为
的最大值为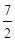 .
.
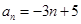 ,
,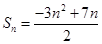 ;(2)
;(2)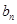 的最大值为
的最大值为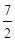 .
.试题分析:本题主要考查等差数列的概念与通项公式、求和公式、不等式等基础知识,同时考查运算求解能力.第一问,利用等差数列的通项公式将
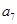 和
和 展开,用
展开,用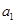 和
和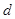 表示,将
表示,将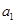 代入,求出
代入,求出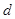 ,代入到等差数列的通项公式和前n项和公式中;第二问,将第一问的结论代入,整理
,代入到等差数列的通项公式和前n项和公式中;第二问,将第一问的结论代入,整理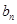 表达式,利用基本不等式求
表达式,利用基本不等式求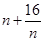 的最小值,从而求出
的最小值,从而求出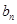 的最大值.
的最大值.试题解析:(Ⅰ) 设公差为
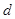 ,由题意知
,由题意知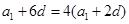 ,
,由
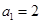 解得
解得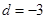 ,
,故
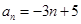 ,
,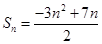 ,
,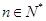 . 8分
. 8分 (Ⅱ) 由(I)得
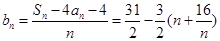 .
.由基本不等式得
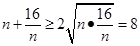 ,
,所以
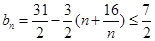 ,又当
,又当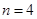 时,
时, .
.从而得
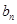 的最大值为
的最大值为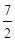 . 14分
. 14分
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
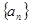 是等差数列,
是等差数列,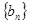 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且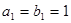 ,
,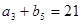 ,
,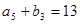 .
.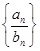 的前
的前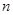 项和
项和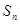 .
.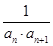 ,其前n项和为Sn.
,其前n项和为Sn.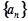 的前
的前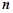 项的和为
项的和为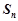 ,且
,且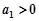 ,
,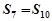 ,则使
,则使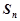 取到最大值的
取到最大值的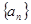 的前
的前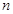 项和为
项和为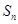 ,若
,若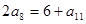 ,则
,则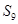 的值等于( )
的值等于( )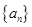 满足
满足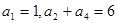 ,且对任意
,且对任意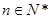 ,函数
,函数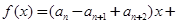
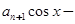
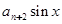 满足
满足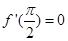 ,若
,若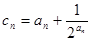 ,则数列
,则数列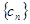 的前
的前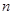 项和
项和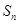 为( )
为( )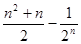
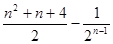
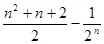
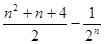
 = .
= .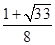
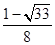
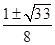
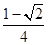
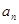 }为等差数列,其公差为-2,且a7是a3与a9的等比中项,
}为等差数列,其公差为-2,且a7是a3与a9的等比中项,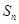 为{
为{