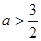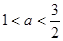题目内容
在平面直角坐标系内,动圆 过定点
过定点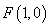 ,且与定直线
,且与定直线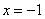 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹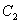 的方程;
的方程;
(2)中心在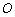 的椭圆
的椭圆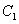 的一个焦点为
的一个焦点为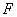 ,直线过点
,直线过点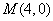 .若坐标原点
.若坐标原点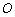 关于直线的对称点
关于直线的对称点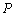 在曲线
在曲线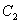 上,且直线与椭圆
上,且直线与椭圆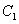 有公共点,求椭圆
有公共点,求椭圆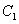 的长轴长取得最小值时的椭圆方程.
的长轴长取得最小值时的椭圆方程.
 过定点
过定点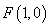 ,且与定直线
,且与定直线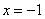 相切.
相切.(1)求动圆圆心
 的轨迹
的轨迹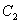 的方程;
的方程;(2)中心在
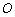 的椭圆
的椭圆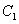 的一个焦点为
的一个焦点为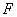 ,直线过点
,直线过点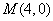 .若坐标原点
.若坐标原点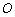 关于直线的对称点
关于直线的对称点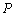 在曲线
在曲线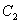 上,且直线与椭圆
上,且直线与椭圆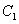 有公共点,求椭圆
有公共点,求椭圆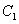 的长轴长取得最小值时的椭圆方程.
的长轴长取得最小值时的椭圆方程. (1) .(2)
.(2)
 .(2)
.(2)
试题分析:⑴由题可知,圆心
 到定点
到定点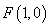 的距离与到定直线
的距离与到定直线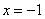 的距离相等
的距离相等 由抛物线定义知,
 的轨迹
的轨迹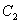 是以
是以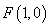 为焦点,直线
为焦点,直线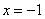 为准线的抛物线
为准线的抛物线 所以动圆圆心
 的轨迹
的轨迹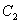 的方程为
的方程为 .
. ⑵解法1、
设
 ,则
,则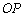 中点为
中点为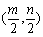 ,因为
,因为 两点关于直线
两点关于直线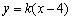 对称,所以
对称,所以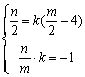 ,即
,即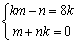 ,解之得
,解之得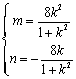 8分
8分将其代入抛物线方程,得:
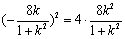 ,所以
,所以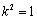 .
. 联立
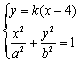 ,消去
,消去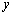 ,得:
,得:
由
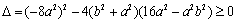 ,得
,得 ,
, 注意到
 ,即
,即 ,所以
,所以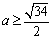 ,即
,即 ,
, 因此,椭圆
 长轴长的最小值为
长轴长的最小值为 .此时椭圆的方程为
.此时椭圆的方程为 .
. 解法2、
设
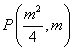 ,因为
,因为 两点关于直线对称,则
两点关于直线对称,则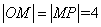 ,
, 即
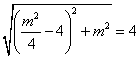 ,解之得
,解之得
即
 ,根据对称性,不妨设点
,根据对称性,不妨设点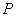 在第四象限,且直线与抛物线交于
在第四象限,且直线与抛物线交于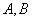 .则
.则 ,于是直线方程为
,于是直线方程为
联立
 ,消去
,消去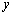 ,得:
,得:
由
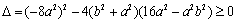 ,得
,得 ,
, 注意到
 ,即
,即 ,所以
,所以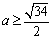 ,即
,即 ,
, 因此,椭圆
 长轴长的最小值为
长轴长的最小值为 . 此时椭圆的方程为
. 此时椭圆的方程为 .
.点评:本题主要考查了圆的切线的性质,圆的标准方程的求法,以及解析几何中的对称性问
题,属于常规题.

练习册系列答案
相关题目
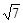 的圆的方程.
的圆的方程.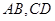 是半径为
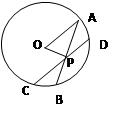
是半径为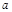 的圆O的两条弦,他们相交于
的圆O的两条弦,他们相交于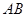 的中点
的中点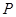 ,
,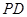 =
=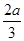 ,
,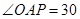 °,则
°,则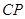 =________
=________
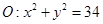 ,椭圆
,椭圆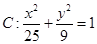 .
.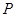 在圆
在圆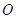 上,线段
上,线段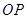 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点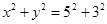 上任意一点
上任意一点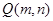 作椭圆
作椭圆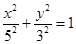 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;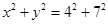 上任意一点
上任意一点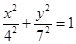 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”.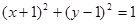 ,圆C2与圆C1关于直线
,圆C2与圆C1关于直线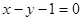 对称,则圆C2的方程为
对称,则圆C2的方程为


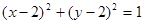
 始终平分圆
始终平分圆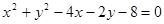 的周长,则
的周长,则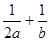 的最小值为
的最小值为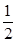



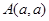 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数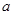 的取值范围为( )
的取值范围为( ) 或
或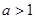
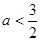
 或
或